三角函数
这个题型有两种考法，大概10%~20%的概率考解三角形，80%~90%的概率考三角函数本身。
(一)解三角形
不管题目是什么，作为被考察者，你要明白关于解三角形，你只学了三个公式——正弦定理，余弦定理和面积公式。所以，解三角形的题目，求面积的话肯定用面积公式。至于什么时候用正弦，什么时候用余弦，如果你不能迅速判断，都尝试一下也未尝不可。
(二)三角函数
三角函数，套路一般是给出一个比较复杂的式子，问函数的定义域、值域、周期频率和单调性等问题。解决方法就是首先利用“和差倍半”对式子进行化简，化简成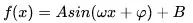
掌握以上公式，关于题型见下图。
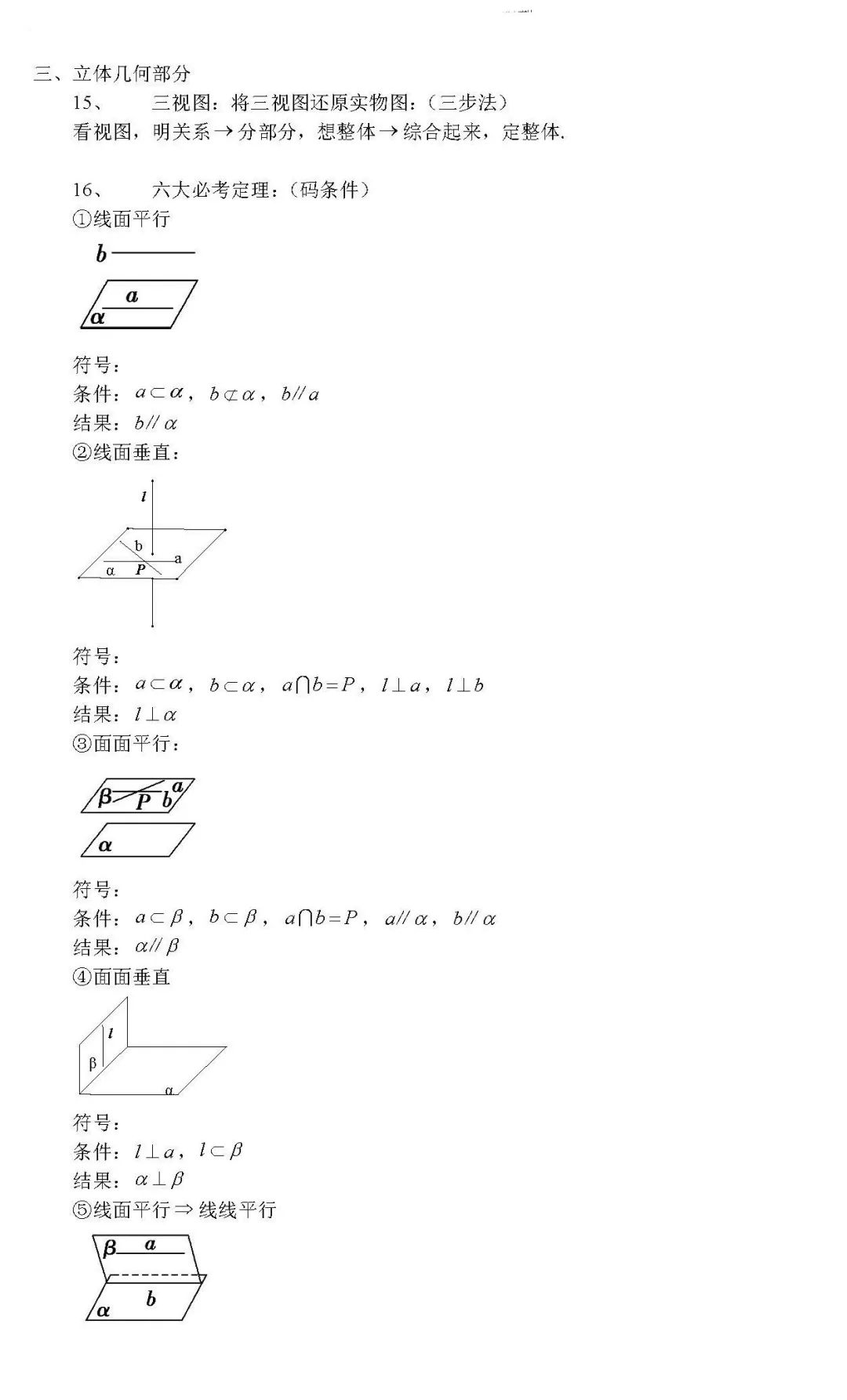
立体几何
相比于前面的三角函数，立体几何题型要稍微复杂一些，可能会卡住一些人。该题通常有2-3问，第一问求某条线的大小或证明某个线/面与另外一个线/面平行或垂直，最后一问求二面角。
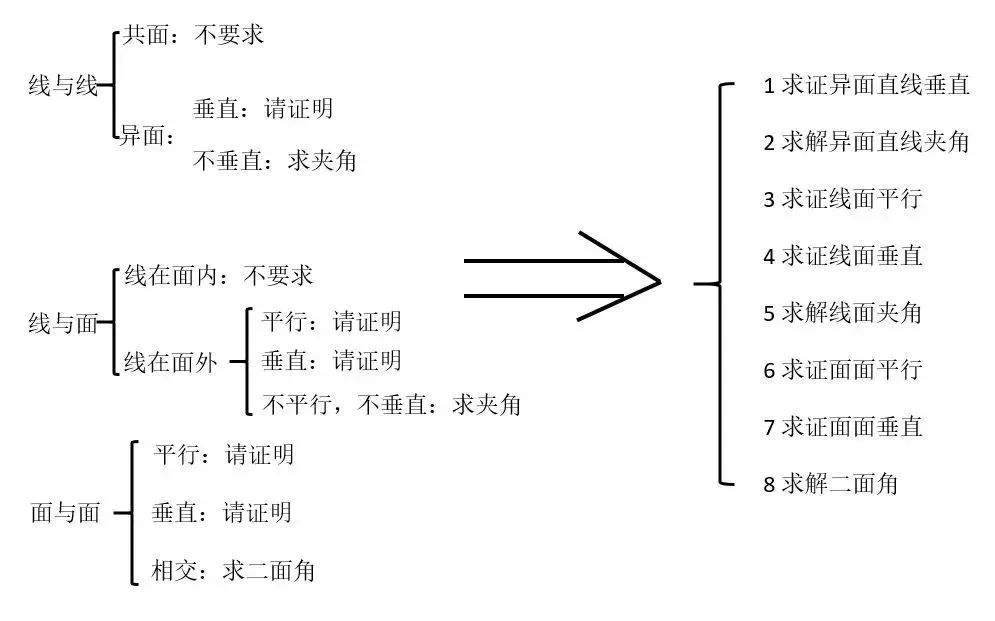
这类题解题方法主要有两种，传统法和空间向量法，其中各有利弊。
(一)向量法：
使用向量法的好处在于没有任何思维含量，肯定能解出最终答案。缺点是计算量大，且容易出错。
应用空间向量法，首先应该建立空间直角坐标系。建系结束后，根据已知条件可用向量确定每条直线。其形式为AB=（a，b，c）然后进行后续证明与求解。
(二)传统法：
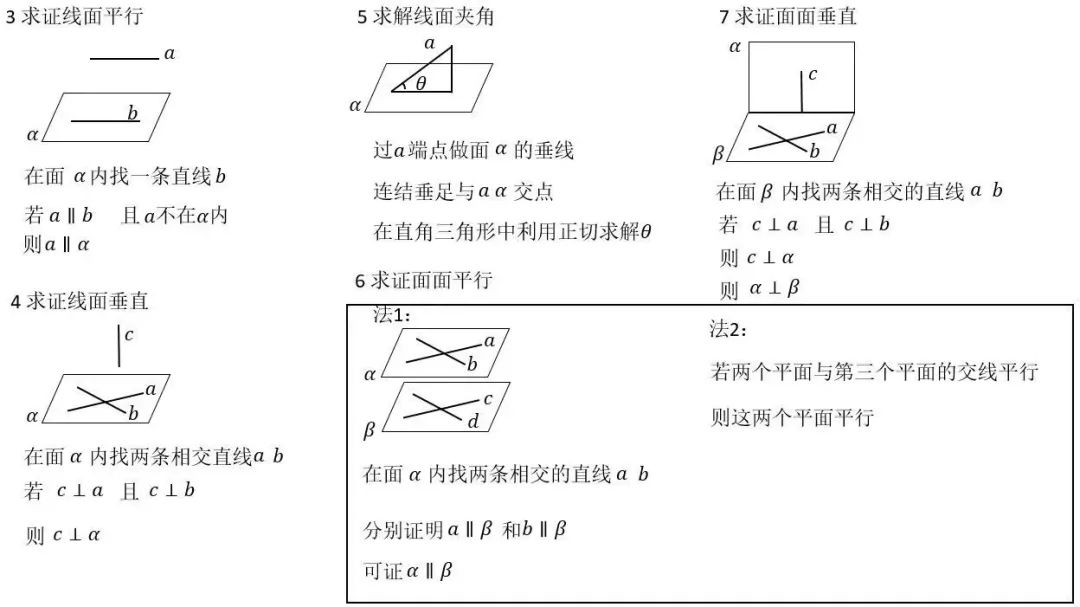
学习立体几何章节，虽然学了很多性质定理和判定定理，但针对高考立体几何大题而言，解题方法基本是唯一的，除了上图6和8有两种解题方法以外，其他都是有唯一的方法。所以，熟练掌握解题模型，拿到题目直接按照标准解法去求解便可。
另外，还有一类题，是求点到平面距离的，这类题百分之百用等体积法求解。
数列
从这里开始，题型难度开始明显增加，但只要掌握了套路和方法，同样并不困难。数列的考察主要是求解通项公式和前n项和。
(一)通项公式
观察题目中给出的条件形式，不同形式对应不同的解题方法。
通项公式的求法我给出了8种，着重掌握上图中的1、4、5、6、7、8，其实4-8可以算作一种。除了以上八种方法，还有一种叫定义法，就是题中给出首项和公差或者公比，按照等差等比数列的定义进行求解。
(二)求前n项和
求前n项和主要有四种方法——倒序相加法，错位相减法，分组求和法，裂项相消法。同样，每种方法都有对应的使用范围。
当然，还有课本上关于等差数列和等比数列求前n项和的基本方法，请大家牢记掌握。
圆锥曲线
高考对于圆锥曲线的考察也是有套路可循的。一般套路就是：前半部分是对基本性质的考察，后半部分考察与直线相交。
如果高考题做得足够多，你会发现后半部分的步骤基本是一致的。即：设直线，然后将直线方程带入圆锥曲线，得到一个关于x的二次方程，分析判别式，韦达定理，利用定理的结果求解待求量。
所以，学好圆锥曲线需要明白三件事：
(一)三种圆锥曲线的性质
在此不再列举，请同学们自行总结。
(二)求轨迹的方法
求动点的轨迹方程的方法有7种，下面将一一介绍。
1.性质法
这类方法最常见，一般设置为第一问，题干中给出圆锥曲线的类型，并给出部分性质，比如离心率，焦点，端点等，根据圆锥曲线的性质求解a,b。
2.定义法
定义法的意思呢，就是题目中给出的条件其实是某种我们学过的曲线的定义，这种情况下，可以根据题目描述，确定曲线类型，再根据曲线的性质，确定曲线的参数。各曲线的定义如下：
到定点的距离为定值的动点轨迹为圆；
到两个定点的距离之和为定值的动点轨迹为椭圆；
到两个定点的距离之差为定值的动点轨迹为双曲线；
到定点与定直线的距离之比为定值的动点轨迹为圆锥曲线；
3.直译法
顾名思义，就是直接翻译题目中的条件。将题目中的文字用数学方程表达出来即可。
4.相关点法
假如题目中已知动点P的轨迹，另外一个动点M的坐标与P有关系，可根据此关系，用M的坐标表示P的坐标，再带入P的满足的轨迹方程，化简即可得到M的轨迹方程。
5.参数法
当动点坐标x、y之间的直接关系难以找到时，可以先找到x、y与另一参数t的关系，得再消去参变数t，得到轨迹方程。
6.交轨法
若题目中给出了两个曲线，求曲线交点的轨迹方程时，应将两动曲线方程中的参数消去，得到不含参数的方程，即为两动曲线交点的轨迹方程。
7.点差法
只要是中点弦问题，就用点差法。
(三)与直线相交
必考题，且每年形式基本一致，先从理论上说说这道题的解题步骤。
步骤1：先考虑直线斜率不存在的情况。求结果。（此过程仅需很简短的过程）
步骤2：设直线解析式为 y=kx+b（随机应变，也可设为两点式）
步骤3：一般，所设直线具有某种特征，根据其特征，消去上式中k或b中的一个。
步骤4：联立直线方程和圆锥曲线方程，得到：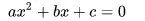
步骤5：求出判别式 △，令 △>0（先空着，必要时候再求 △>0 时的取值范围）
步骤6：利用韦达定理求出 x1x2，x1+x2（先空着，必要时再求y1y2）
步骤7：翻译题目，利用韦达定理的结果求出所求量。
函数与导数
导数这块的步骤也是固定的，导数与函数的题型，大体分为三类。
1.关于单调性，最值，极值的考察；
2.证明不等式；
3.函数中含有字母，分类讨论字母的取值范围；
无论是哪种题型，解题的流程只有一个，如下图所示。
例题比较简单，但是注意两点：一是任何导数题的核心步骤都是以上四部，二是时刻提醒自己定义域。以上例题属于第一类题型。
第二类题型，证明不等式，需要先移项，构造一个新函数，可以使不等号左边减去右边，构成的新函数，利用以上四个步骤分析新函数的最值与0的大小关系，可以得证。此为作差法。还有一种方法叫作商，即左边除以右边，其结果与1做对比。不过此方法不建议使用，因为分母有可能为0，或者正负号不确定。
还要注意逻辑。如果证明 A ≤ B，新函数设为 A - B，那么，需要 A - B的最大值小于等于0。
第三类问题，求字母的取值范围。先闭着眼睛当成已知数算，算完以后列表，针对列表中的结果进行分情况讨论。（一般，题目都会写明字母不为0）
以上就是为各位同学总结的题型和解题套路，并没有把所有的题型完整总结，只是提供一个思路和示范，此外下方还为大家整理归纳了高中数学100个核心考点，同学们可以按照这种模式自行总结。最后，重申三点：记住基础知识素材，总结题型，提取解题策略。
高中数学100个核心考点全汇总
高中数学 高考数学 高考数学 高中数学
微信扫一扫打赏