苏教版高中数学必修二《13.3.1空间图形的表面积》试题
13.3.1空间图形的表面积
一、单选题
1.已知圆锥的轴截面是等腰直角三角形,且圆锥的母线长为2,则圆锥的侧面积是().
A.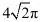 B.2C.
B.2C. D.
D.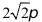
【答案】D
【解析】
【分析】
先求出底面圆周长,再计算圆锥侧面积即可.
【详解】
如图,由题意知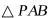 为等腰直角三角形,则
为等腰直角三角形,则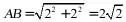 ,底面圆周长为
,底面圆周长为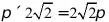 ,
,
故圆锥的侧面积为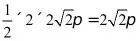 .
.
故选:D.
2.攒尖是我国古代建筑中屋项的一种结构样式,宋朝时称“撮尖”,清朝时称“攒尖”,通常有圆形攒尖、三角攒尖、四角攒尖、八角攒尖,也有单檐和重檐之分,多见于亭阁式建筑,园林建筑,下面以圆形攒尖为例.如图,亭阁式建筑屋项部分的轮廓可近似看作一个圆锥,其底面半径约为4米,母线长约为6米,则该圆形攒尖侧面的面积约为()

A.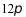 B.
B.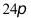
C.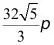 D.
D.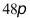
【答案】B
【解析】
【分析】
根据圆锥侧面积公式,求解.
【详解】
由条件可知,圆锥的底面半径 ,母线
,母线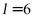 ,
,
则圆锥侧面积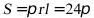 .
.
故选:B
3.正四棱台上、下底面边长分别为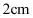 ,侧棱长
,侧棱长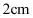 ,则棱台的侧面积为()
,则棱台的侧面积为()
A.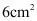 B.
B.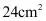 C.
C.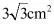 D.
D.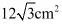
【答案】D
【解析】
【分析】
由棱台的性质和勾股定理求得棱台的斜高,再由棱台的侧面积公式,计算可得所求值.
【详解】
解:设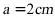 ,可得正四棱台的斜高为
,可得正四棱台的斜高为 ,
,
所以棱台的侧面积为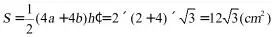 .
.
故选: .
.
4.若圆锥的轴截面为等边三角形,则该圆锥的侧面积与表面积的比值为()
A.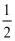 B.
B.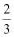 C.
C.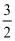 D.2
D.2
【答案】B
【解析】
【分析】
圆锥的侧面积为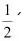 底面周长
底面周长 母线长.侧面积为底面积加侧面积,相比即可得到答案.
母线长.侧面积为底面积加侧面积,相比即可得到答案.
【详解】
设底面半径为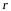 ,底面面积为
,底面面积为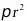 ,圆锥的侧面积为
,圆锥的侧面积为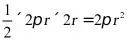 ,圆锥的表面积为底面积加侧面积为:
,圆锥的表面积为底面积加侧面积为: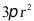 .
.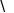 该圆锥的侧面积与表面积的比值为
该圆锥的侧面积与表面积的比值为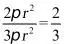 .
.
故选:B.
5.一个圆台的母线长等于上、下底面半径和的一半,且侧面积是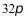 ,则母线长为()
,则母线长为()
A.2B.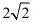 C.4D.8
C.4D.8
【答案】C
【解析】
【分析】
根据圆台的侧面积公式可得答案.
【详解】
设圆台的母线长为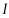 ,上,下底面的半径分别为
,上,下底面的半径分别为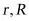 ,则
,则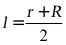
圆台的侧面积为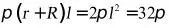 ,解得
,解得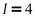
故选:C
6.已知圆锥轴截面是等腰直角三角形,一个正方体有四个顶点在圆锥的底面上,另外的四个顶点在圆锥的侧面上(如图),则圆锥与正方体的表面积之比为()
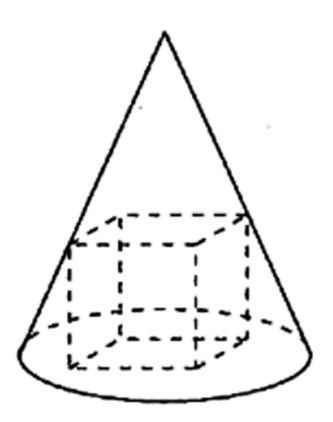
A.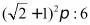 B.
B.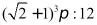 C.
C.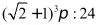 D.以上答案都不对
D.以上答案都不对
【答案】B
【解析】
【分析】
设圆锥的底面半径为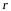 ,正方体的边长为
,正方体的边长为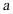 ,求出
,求出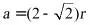 ,再求出圆锥和正方体的表面积化简即得解.
,再求出圆锥和正方体的表面积化简即得解.
【详解】
解:设圆锥的底面半径为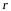 ,正方体的边长为
,正方体的边长为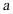 ,由轴截面得
,由轴截面得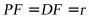 ,
,
因为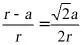 ,所以
,所以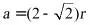 ,
,
所以圆锥的表面积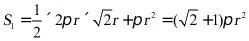 ,
,
正方体的表面积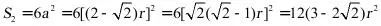
所以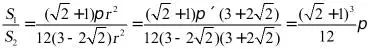 .
.
故选:B
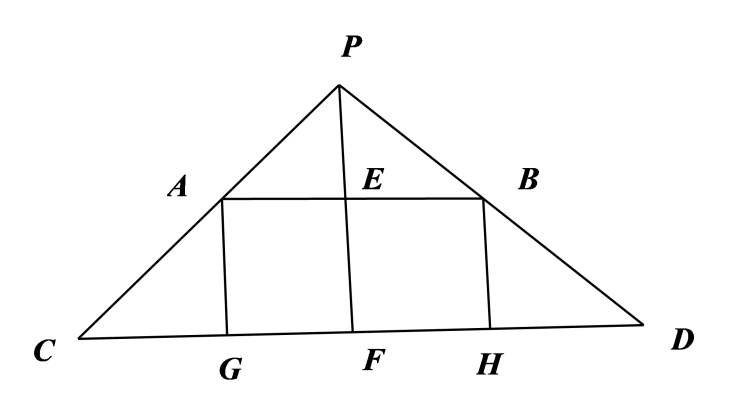
二、填空题
7.若五棱台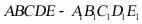 的表面积是30,侧面积是25,则两底面面积的和为______.
的表面积是30,侧面积是25,则两底面面积的和为______.
【答案】5
【解析】
【分析】
由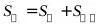 即求.
即求.
【详解】
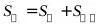 ,
,
则 .
.
故答案为:5.
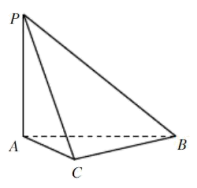
8.词语“堑堵”、“阳马”、“鳖臑”等出现自中国数学名著《九章算术・商功》,是古代人对一些特殊锥体的称呼.在《九章算术・商功》中,把四个面都是直角三角形的四面体称为“鳖臑”.现有如图所示的“鳖臑”四面体PABC,其中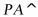 平面
平面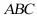 ,则四面体PABC的外接球的表面积为______.
,则四面体PABC的外接球的表面积为______.
【答案】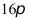
【解析】
【分析】
确定外接球球心求得球半径后可得表面积.
【详解】
由于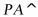 平面
平面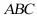 ,因此
,因此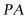 与底面上的直线
与底面上的直线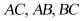 都垂直,
都垂直,
从而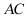 与
与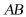 不可能垂直,否则
不可能垂直,否则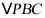 是锐角三角形,由于
是锐角三角形,由于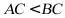 ,因此有
,因此有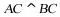 ,
,
而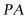 与
与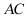 是平面
是平面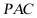 内两相交直线,则
内两相交直线,则 平面
平面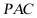 平面
平面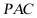 ,所以
,所以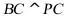 ,
,
所以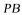 的中点
的中点 到
到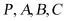 四个点的距离相等,即为四面体PABC的外接球球心.
四个点的距离相等,即为四面体PABC的外接球球心.
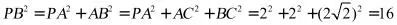 ,
,
所以所求表面积为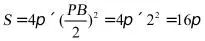 .
.
故答案为: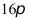 .
.
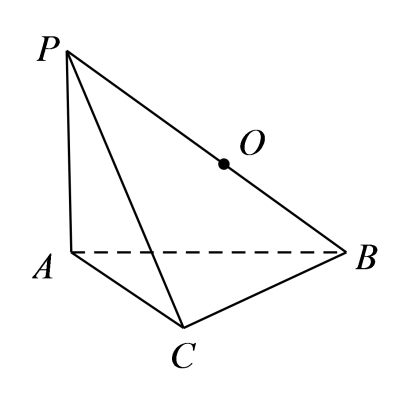
三、解答题
9.已知在正三棱柱 中,侧棱长
中,侧棱长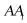 为3,H、G分别是AB,中点.
为3,H、G分别是AB,中点.

(1)证明: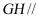 平面
平面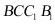 ;
;
(2)若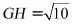 ,求此三棱柱的侧面积.
,求此三棱柱的侧面积.
【答案】(1)证明见解析
(2)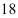
【解析】
【分析】
(1)取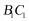 的中点
的中点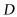 ,连接
,连接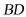 、
、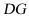 ,即可得到四边形
,即可得到四边形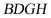 为平行四边形,即
为平行四边形,即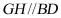 ,即可得证;
,即可得证;
(2)由(1)可得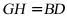 ,根据正三棱柱的性质及勾股定理求出
,根据正三棱柱的性质及勾股定理求出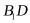 ,即可求出底面边长,再根据侧面积公式计算可得;
,即可求出底面边长,再根据侧面积公式计算可得;
(1)证明:取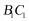 的中点
的中点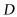 ,连接
,连接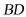 、
、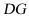 ,因为
,因为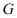 为
为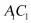 的中点,
的中点,
所以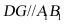 且
且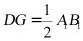 ,又
,又 是
是 的中点,
的中点,
且三棱柱 是正三棱柱,
是正三棱柱,
所以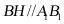 且
且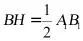 ,所以
,所以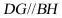 且
且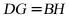 ,
,
所以四边形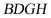 为平行四边形,所以
为平行四边形,所以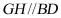 ,
,
因为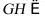 平面
平面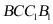 平面
平面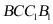 ,所以
,所以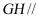 平面
平面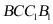 ;
;
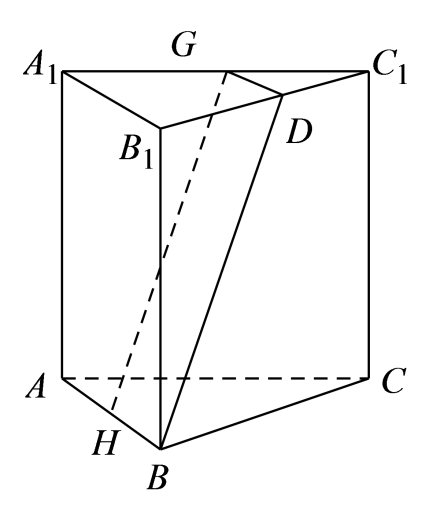
(2)解:由(1)可知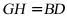 ,所以
,所以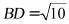 ,又
,又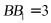 ,
,
正三棱柱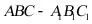 中侧棱垂直于底面且底面是正三角形,
中侧棱垂直于底面且底面是正三角形,
所以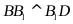 ,所以
,所以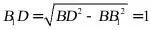 ,即
,即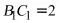 ,
,
所以棱柱的侧面积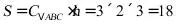
10.如图,圆锥底面半径为1,高为2.
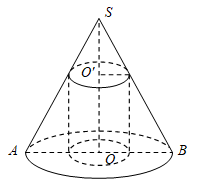
(1)求圆锥内接圆柱(一底面在圆锥底面上,另一底面切于圆锥侧面)侧面积的最大值;
(2)圆锥内接圆柱的表面积是否存在最大值?说明理由;
(3)若圆锥的底面半径为a,高为b,试讨论圆锥内接圆柱的全面积是否存在最大.
【答案】(1)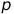
(2)不存在,理由见解析
(3)存在最大值
【解析】
【分析】
(1)依题意作出圆锥的轴截面,设内接圆柱底面半径为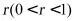 ,高为h,利用三角形相似得到
,高为h,利用三角形相似得到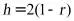 ,再利用基本不等式求出面积的最大值;
,再利用基本不等式求出面积的最大值;
(2)由(1)可得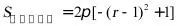 ,根据二次函数的性质判断可得;
,根据二次函数的性质判断可得;
(3)依题意可得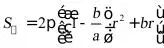 ,根据二次函数的性质计算可得;
,根据二次函数的性质计算可得;
(1)解:作出轴截面如下图所示,
设内接圆柱底面半径为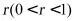 ,高为h,,由
,高为h,,由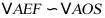 ,所以
,所以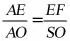 ,所以
,所以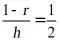 ,所以
,所以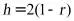
当且仅当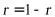 ,即
,即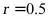 时等号成立,此时侧面积最大;
时等号成立,此时侧面积最大;
(2)
解:由(1)可得
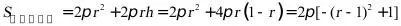 ,而
,而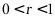 ,故不存在最大值;
,故不存在最大值;
(3)解:设圆柱底面半径为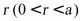 ,高h,由
,高h,由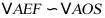 ,所以
,所以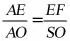 ,所以
,所以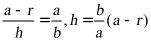
所以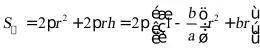
当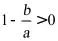 ,即
,即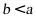 ,二次函数
,二次函数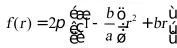 开口向上,在
开口向上,在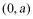 内无最大值
内无最大值
当 ,即
,即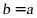 ,一次函数
,一次函数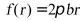 在
在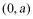 内也无最大值
内也无最大值
当 ,即
,即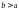 ,二次函数开口向下,若区间内存在最大值,则对称轴
,二次函数开口向下,若区间内存在最大值,则对称轴
所以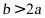 ,综上当且仅当
,综上当且仅当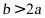 (圆锥高大于底面半径)时,圆锥的内接圆柱的全面积存在最大值;
(圆锥高大于底面半径)时,圆锥的内接圆柱的全面积存在最大值;
本文由小编发布,不代表一本线高考网立场,转载联系作者并注明出处:https://www.yibenxian.com/gaozhong/56576.html

