高中数学奥林匹克竞赛教程基础篇,10章28讲
第一章集合、常用逻辑用语、算法
第一讲集合
知识归纳
集合的运算是高考和竞赛的热点之一, 考查内容包括对子集、交集、并集、全集、补集概念的理解, 集合间的转化, 集合运算性质的应用等.
1. 集合的概念.
集合是数学中的原始概念, 其表示方法有列举法、描述法和韦恩 (Venn) 图表示法, 常用的集合还有约定的字母符号表示 (如实数集用 ,空集用 表示等).
2. 集合之间的关系.
元素与集合之间具有"属于()"或"不属于()"的关系,集合与集合之间的关系包括包含关系、相等关系和不包含关系.包含关系与子集概念等价,即集合包含于集合 B 等价于 是 的子集,记作 集合 真包含于集合 等价于 是 的真子集,记做 若 且,则集合 相等,记做
3. 集合的运算.
除教科书上介绍的运算律外,还有下面的两个运算律 ( 是全集):
(1)分配律 ,
(2)摩根律,
4. 有限集的子集的个数.
若有限集 含有 个元素,则 的子集有 个,真子集有 个,非空子集有 个.
5. 有限集的元素个数.
对任意两个有限集合 ,有 ,. 此结论可以推广到任意 个有限集合 (称为容斥原理).
典型例题
例 1
已知集合 . 集合 满足下列条件: 若集合 中各元素都加 2,就变为 的一个子集; 若集合 中各元素都减 2,就变为 的一个子集. 求集合 .
解
集合 中各元素都减 2,得 ; 集合 中各元素都加 2,得 , . 由题意,得集合 ,且 ,
,且 . ,或 ,或 .
评注
通过本题,我们体会到列举法能直观地表示集合. 根据条件写出集合 所属的两个集合,而集合 是这两个集合交集的子集,得到交集即可得到集合 .
例 2
已知集合,求实数 的值.
分析 可转化为 ,化简集合 即可.
解
由 ,得 ,其中 .
为了求集合 ,分下列两种情况讨论: (1) 当 时, ,适合条件. (2) 当 时, ,要使 ,只需 ,或 ,或 .
综上所述, ,或 ,或 .
评注
有关两个集合关系的问题不可忽视空集、全集的情况,本题极易漏掉 .
例 3
(1) 已知集合, 求 .
(2)已知集合,求 .
(3)已知集合,求 .
(4)已知集合, 求 .
解
(1) 集合 是二次方程的解集,求 即求两个二次方程的公共解构成的集合. 由 ,得 ,或 . 由 ,得 ,或 .
.
(2)集合 是二次函数的函数值 的取值范围, 即为两个二次函数值取值范围的公共部分构成的集合.
,
.
(3)由 ,得 是变量 取自然数时,所对应的整数值构成的集合.
.
(4)集合 表示抛物线上的点集 (或二元二次方程的解集),
是两条抛物线的交点构成的集合.
由 $\left{
\right.\ 解得\left{\right.\ 或\left{\mspace{6mu}\therefore\mspace{6mu} A \cap B = {(3,12),( - 3,0)} \right.\ $ .评注
(1) 用描述法表示集合 时,要有代表元素 及它所具有的性质 这两项内容.
(2)描述法表示集合具有概括、简练和抽象的特点, 列举法表示集合具有直观、清晰和可数的特点, 解题时要根据需要进行互化.
例 4
已知集合 0,x \in \mathbf{R}\}" style="margin: 0px; padding: 0px; outline: 0px; max-width: 100%; cursor: pointer; overflow-wrap: break-word !important;"> 0,x \in \mathbf{R}\}" style="margin: 0px; padding: 0px; outline: 0px; max-width: 100%; overflow-wrap: break-word !important;">,且 ,求实数 的取值范围.
分析 由 是一元二次方程的解集, 是正实数集,得 等价于二次方程无解或有两个非正实数解.
解
当 时,<span data-formula="\Delta = (k - 3)^{2} + 16k = k^{2} + 10k + 9 <span data-formula="\Delta = (k - 3)^{2} + 16k = k^{2} + 10k + 9 ,解得 <span data-formula="- 9 < k <span data-formula="- 9 < k .
当 时, 有两个非正实数解,则
实数的取值范围是.
评注
集合是一种数学语言, 根据集合运算进行等价转化是解决集合运算问题的基本思路. 而理解问题中集合表示的对象, 联想有关知识, 是正确转化的关键.
例 5
已知全集<span data-formula="U = \left\{ x \mid x^{2} <span data-formula="U = \left\{ x \mid x^{2} , ,求 和 .
分析 题中出现 等多个集合,可以运用 Venn 图解题.
解
① 全集<span data-formula="U = \left\{ x \mid x^{2} <span data-formula="U = \left\{ x \mid x^{2} .
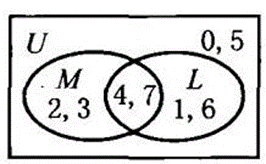
图 1-1
②如图 1-1,将, 中的元素在图中依次定位.
③将元素 4,7 定位.
④根据图中元素的位置,得 .
评注
集合问题比较抽象, 解题时应尽可能借助韦恩图、数轴等直观图形, 利用数形结合思想将抽象问题直观化、明朗化, 从而使问题得到解决.
例 6
设集合 是 的子集,且满足条件: 当 时, ,则 中元素的个数最多是多少个?
解
由题设知, 与 这两个数中至少有一个不属于 .
时, 一定不属于 .
同理, ,当 时, 与 不能同时属于 ,此时至少有 134 个数不属于 ,于是, .
因为可取 ,所以 的最大值为 1884 .
例 7
设集合 .
(1)当 取何值时, 为含有 2 个元素的集合?
(2)当 取何值时, 为含有 3 个元素的集合?
分析 因为 ,所以只要求出 和 中的元素,再分别加以讨论即可.
解
与 分别为方程组
( I ) $\left{
\right.\ \left{\right.\ $ 的解集.由 ,得 或 .
由 (II),得 或 .
(1)要使 含有 2 个元素,只需① $\left{
\right.\ 或②\left{\right.\ $由 ①,得 . 由②,得 .
故当 或 1 时, 含有 2 个元素.
(2)要使 含有 3 个元素,只需 ,解得 .
故当 时, 含有 3 个元素.
评注
解决本题的关键是合理利用集合的运算律.
例 8
已知集合 0\},B = \{(x,y)||xy \right| + 1 = |x| +" style="margin: 0px; padding: 0px; outline: 0px; max-width: 100%; cursor: pointer; overflow-wrap: break-word !important;"> 0\},B = \{(x,y)||xy \right| + 1 = |x| +" style="margin: 0px; padding: 0px; outline: 0px; max-width: 100%; overflow-wrap: break-word !important;"> . 若 是平面上正八边形的顶点所构成的集合,求 的值.
分析 由已知条件知, 是平面上正八边形的顶点所构成的集合,故需先求出 的具体元素,然后利用数形结合思想解题.
解
由集合 ,得 .
先求 位于第一象限内的点.
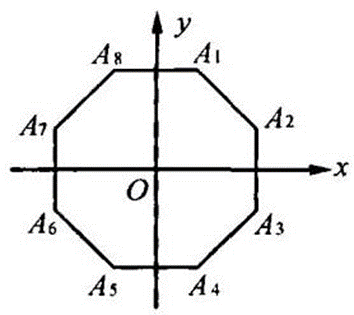
图 1-2
解方程组 $\left{
\right.\ 得\left{\right.\ 或\left{\right.\ 于是得到A \cap B在第一象限内的两点(1,a - 1),(a - 1,1)注意到集合A \cap B中的元素满足的式子都是绝对值方程所以与第一象限内两点关于x轴、原点、y轴对称的个点仍然是A \cap B$ 中的元素, 如图 1-2 所示.下面讨论 取何值时,这 8 个点构成正八边形.
①若点 ,则点 . 于是 ,得<span data-formula="a = 2 + \sqrt{2}\left( a = 2 - \sqrt{2} <span data-formula="a = 2 + \sqrt{2}\left( a = 2 - \sqrt{2} 舍去.
②若点 ,则点 . 于是 ,得<span data-formula="a = \sqrt{2}\left( a = - \sqrt{2} <span data-formula="a = \sqrt{2}\left( a = - \sqrt{2} 舍去 .
综上所述, 的值为 或 .
评注 解本题的关键是用代数方法(解方程组)求出正八边形在第一象限内的两个顶点 的坐标,然后利用对称性求出顶点 的坐标,再利用 ,构造关于 的方程. 本题还有一种解法: 点集 中的点构成顶点为 的正方形的四条边; 对于点集 ,可将 变形为 ,所以点集 中的点构成四条直线 . 以下可以利用数形结合思想,请读者自行完成.
例 9
集合 满足下列条件:
① .
② <span data-formula="A_{i} \cap A_{j} = \varnothing,1 \leq i <span data-formula="A_{i} \cap A_{j} = \varnothing,1 \leq i .
那么称 为集合 的一个 划分.
求最小正整数 ,使得对 的任意一个 14 划分 ,一定存在某个集合 ,在 中有 2 个元素 ,满足 <span data-formula="b <span data-formula="b .
解
(1) 若 <span data-formula="m <span data-formula="m ,令,则 <span data-formula="\forall b <span data-formula="\forall b , 14),均有 a > b" style="margin: 0px; padding: 0px; outline: 0px; max-width: 100%; cursor: pointer; overflow-wrap: break-word !important;"> a > b" style="margin: 0px; padding: 0px; outline: 0px; max-width: 100%; overflow-wrap: break-word !important;"> ,且 . 故 <span data-formula="b \leq a - 14 <span data-formula="b \leq a - 14 .
(2)若 ,则对 的任意划分 ,数 中,必有两个数属于同一个 ,它们满足<span data-formula="b <span data-formula="b .
例 10
当 时, ,非空子集共有 15 个. 它们的全部 "交替和"如下:
解
方法导引与拓展
解决有关集合之间的关系问题, 要注意抓住元素这个关键, 同时不能忽视空集这个特殊情况, 否则极易漏解 (如例 2 、例 4).
集合问题是综合问题, 它可能涉及代数、几何、数论、计数以及其他数学内容和数学思想方法. 如例 3 、例 4 涉及函数、方程, 例 5 、例 8 运用了数形结合思想, 例 10 运用了映射思想等.
巩固练习
1. 定义集合运算: . 设集合 , 则集合 的所有元素之和为 ( ).
5. 集合 的并集 ,当 时,将 与 视为不同的集合对,则这样的集合对 的个数是 ( ).
6. 函数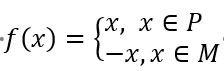 ,其中 为实数集 的两个非空子集. 又规定 . 给出下列四个判断:
,其中 为实数集 的两个非空子集. 又规定 . 给出下列四个判断:
9. 某班 41 名学生参加数学、生物、化学 3 个科目的考试, 考试不及格的学生人数如下表: 科目 数学 生物 化学 数学、生物 数学、化学 生物、化学 数学、生物、化学
11. 已知非空集合 ,且当 时,必有 ,那么符合要求的 A 共有______个.
14. 已知一个集合含有 10 个互不相同的两位数, 求证: 这个集合必有两个无公共元素的子集, 这两个子集的各元素之和相等.
15. 已知集合 ,其中 . 由 中的元素构成两个集合:, 其中 是有序数对,集合 和 中的元素个数分别为 和 . 若对于任意 , 总有 ,则称集合 具有性质 .
本文由小编发布,不代表一本线高考网立场,转载联系作者并注明出处:https://www.yibenxian.com/history/57207.html

