24年高考在今天就基本上圆满结束了。从命题来看，理科较为简单，而文科则难度较大，符合大学理工类专业的扩招目的。所以今年志愿填报，选物理、化学科目的考生在专业选择和录取上一定是非常占据优势的。新高考数学I、II卷，解答题部分，I卷要较II卷难。是不是那个省份的考生多，题目就相对难呢（只是猜测）。

【考情分析】全国新高考I、II卷，解答题的15题考察的解三角形，都是常规的、非常基础的考法，在之前的文章中一再强调，解三角形本身是最简单的一个平面几何问题。高考数学卷一定考得是正、余弦定理的应用。因为这两个公式将边、角统一起来了。新高考I卷同时考察了这两个定理。II卷中仅考察了正弦定理的使用。

【解析】第一问基本不用思考，配凑即可（略）（答案：π/6，注意尽量不要写成30^o）。第二问，要求周长，必然要求出三边关系，余定理有平方，直接上正弦定理，该三角形为定三角形，各角非常容易求出。（答案：2+√6+3√2）本题实际上就是送分题。

【考情分析】导数题目在往年新高考改革前，都是作为压轴题目出现的。大家翻看一下22年导数题，当时能拿到该题满分的考生寥寥无几。而24年作为高考改革元年，无论是I卷还是II卷，导数解答题还是非常容易得分的。

历年的导数命题更偏向于应用数学，而非逻辑推理的理论题目，根据改革的趋势，向“强基”迈进，必然会对逻辑推理模块予以重点考察。可以遇见的是数列、概率、排列组合等重逻辑推理的模块会走上高考的舞台作为重头戏。

【解析】函数解析式形式就很简单，只有一个参数，很讨喜。第一问考的是导数的几何意义（略）。第二问利用导数求极值。先需要利用函数的导数找到f(x)极值处对应的自变量x（横坐标），再根据x找函数值f(x)，函数的映射关系不都是这样吗。将自变量带到f(x)中，获得了一个关于参数a的解析式。根据这个解析式，结合题目给出的条件f(x)<0，非常容易的获得了a的范围。（答案：a>1）

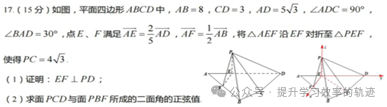
【考情分析】I、II卷立体几何均以椎体作为载体。第一问都是考位置关系。第二问也都是考法向量的应用（常规做法也能解，推荐大家使用向量的法向量解题，遇到常规操作复杂的建系运用法向量计算量和准确率会有很大优势）

【解析】第一问位置关系的证明有平行、垂直、相交（很少考，但会证平行垂直，反证法可以搞定相交）。证明两线垂直方法很多（Ex：直径对应的圆周角、直角三角形、三垂线定理、线面垂直…），题目条件给出了△AEF边角关系，EF利用余弦定理很容易得出（我说怎么第15题只考正弦定理呢，原来余弦定理藏在这了。）进一步证明该三角形为直角三角形即可。

第二问先证EF、ED、EP相互垂直（三垂线），由此以E点建系，列出个点的坐标，为求法向量做准备（大家之所以不愿意使用法向量，实际上是对法向量的本质没有理解透彻，之前文章有分享，感兴趣的可以找一下）本题的法向量求法和相关运算与前几天讲的新I卷大体相同，不再赘述。（答案：sinα=8√65/65）

【考情分析】看到这道题，还以为拿到假卷了，还是那种熟悉的味道（个人认为第二问就是简单的套公式计算，且考法单一，该题很一般）。之前在文章中说过赛制的问题。考察的核心就是最简单的伯努利实验。本题解题的关键就是由第一阶段进入第二阶段的条件（三次投球至少投中一次，限定词很关键。其次，比赛成绩是第二阶段得分的总和。）如果对体育感兴趣的同学，这个题目不难理解，就是淘汰赛和决胜局的问题吧。

【解析】第一问比赛不少于5分的概率为P=(1-0.6³)(1-0.5³)。转化为考虑极端情况都没有投中

第二问第1问【分类讨论】题目问那个队先参加比赛，转化为分别先求出这两个队先参加比赛时，可以拿到15分的概率，然后对起进行比较即可。设甲先参加第一阶段比赛，甲乙所在队比赛成绩15分的概率为P_甲=[1-(1-p)³]q³，同理乙先参加第一阶段比赛，P_乙=[1-(1-q)³]p³。进一步P_甲-P_乙，结合0<p<q，是否大于0即可。

第二问的第2小问考的是关于数学期望的。关键是定义X的可能取值。本题显然只有0,5,10,15这4中情况。与第1小问一样，先分别求出甲乙各自先参加第一阶段比赛的期望。

甲先参加，P(X=0)=(1-p)³+[1-(1-p³)][1-q³]；P(X=5)=[1-(1-p³)]C₃¹q(1-q)²；P(X=10)= [1-(1-p³)]C₃²(1-q)；P(X=15)= [1-(1-p³)]q³,E(X)=15(p³-3p²+3p)q。同理乙先参加E(Y)= 15(q³-3q²-3q)p（连算都不用算将p，q相互代替即可）。E(X)-E(Y)>0

【考情分析】I卷是数列的新定义（可分数列），II卷是以圆锥曲线为载体，第二问同样考察数列。而以圆锥做载体考察数列，在早期的全国卷考过（可以查一下99年全国卷）不新鲜。本题解题的关键是“坐标变换的定义”。其中第三问与I卷一样有难度。

【解析】点在双曲线上，可以获得具体的双曲线，m=9。对于第一问，一直斜率的情况下又过定点直接写出该直线y-4=（x-5）/2。联立求得交点坐标。就是送分的。

第二问与数列相关。比I卷简单多了，至少大家看一遍就明白。点坐标的关系转化为斜率关系即可。P_n(x_n,y_n)关于Y轴的对称点为Q_n-1（-x_n，y_n），点P_n-1（x_n-1，y_n-1）与Q_n-1在斜率k的直线上。即(y_n-y_n-1)/(-x_n-x_n-1)=k。有了这个式子（看结构）结合两个点在双曲线上，可以利用平方差公式获得（x+y）(x-y)的形式。整理一下就获得了（x_n-y_n）/(x_n-1-y_n-1)=(1+k)/(1-k)

第三问可以通过线平行关系，也可以求三角形顶点坐标利用向量表达面积来处理。今天就到这吧，下一篇再分享。