2020年安徽省芜湖市无为中学自主招生数学试卷
2020年安徽省芜湖市无为中学自主招生数学试卷
一、选择题,每小题都给出代号为A、B、C、D的四个选项,其中只有一个是正确的,请把正确选项的代号写在题后的括号内,每一小题,选对得4分,不选、选错或选出的代号超过一个的(不论是否写在括号内)一律得0分。
1.(4分)在2﹣3,,(﹣2)﹣3,这四个数中,最小的是( )
A.2﹣3B.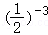 C.(﹣2)﹣3D.
C.(﹣2)﹣3D.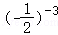
2.(4分)在新冠疫情阻击战中,我国有400万名社区工作者默默无闻地奋战在几十万个社区.将400万用科学记数法表示为( )
A.4×105B.4×106C.4×107D.4×108
3.(4分)下列几何体的左视图是矩形的是( )
A.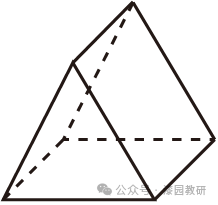 B.
B.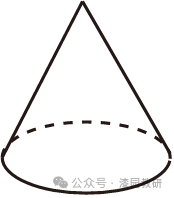 C.
C.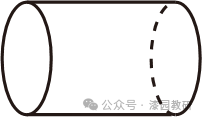 D.
D.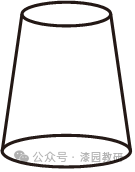
4.(4分)某校对180名初中毕业生进行了一次视力抽样调查,绘制出频数分布直方图(不完整)如图所示,设这次抽样调查所得数据的中位数为x,根据图中的信息判断x的取值范围是( )
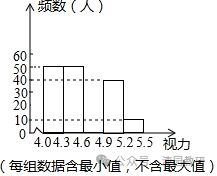
A.0≤x<4.3B.4.3≤x<4.6C.4.6≤x<4.9D.4.9≤x<5.2
5.(4分)我国古代数学的许多创新和发展都位居世界前列,如南宋数学家杨辉(约13世纪)所著的《详解九章算术》一书中,用如图的三角形解释二项式和(a+b)n的展开式的各项系数,此三角形称为“杨辉三角”,若“杨辉三角”中第n行的各数之和比上一行各数之和大64,则n的值为( )

A.7B.8C.9D.10
6.(4分)新定义一种运算“⊗”,其运算法则为:a⊗b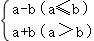 ;例如:1⊗2=﹣1,2⊗1=3.已知a⊗(﹣5)=2,则a的值为( )
;例如:1⊗2=﹣1,2⊗1=3.已知a⊗(﹣5)=2,则a的值为( )
A.3B.﹣3C.7D.﹣7
7.(4分)已知关于x的一元二次方程(a﹣b)x2+(c﹣a)x+(b﹣c)=0有两个相等的实数根且实数a,b,c互不相等,则下列结论一定成立的是( )
A.2a=b+cB.2b=a+cC.2c=a+bD.b2﹣4ac=0
8.(4分)已知x>0,且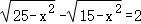 ,则与x最接近的整数是( )
,则与x最接近的整数是( )
A.4B.3C.2D.1
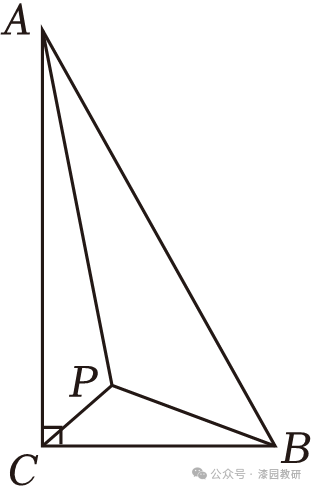
9.(4分)如图,在△ABC中,∠ACB=90°,∠BAC=30°,BC=1,P为△ABC内一点,分别连接PA、PB、PC.当∠APB=∠BPC=∠APC时,PA+PB+PC的值为( )
A.2B.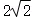 C.
C.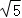 D.
D.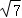
10.(4分)如图,在△ABC中,CD⊥AB于D,AD=9,DB=3,CD=6,矩形的顶点E与A点重合,EF=8,EH=4,将矩形EFGH沿AB平移,当点E与点B重合时,停止平移,设点E平移的距离为x,矩形EFGH与△ABC重合部分的面积为y,则y关于x的函数图象大致为( )
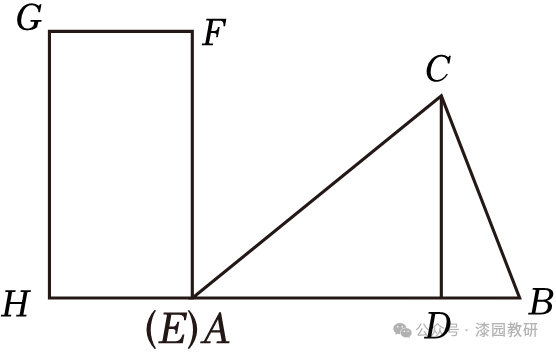
A.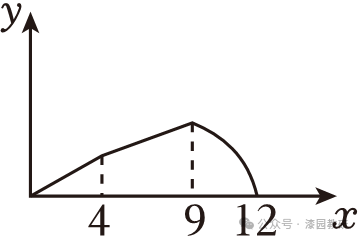 B.
B.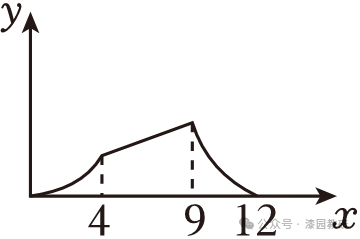
C.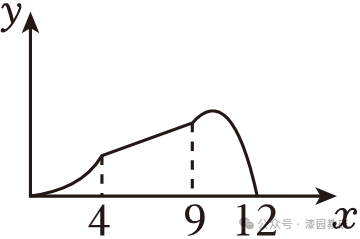 D.
D.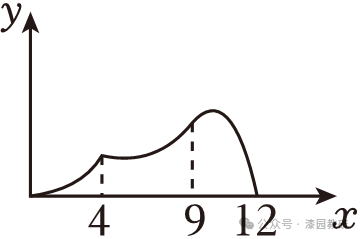
二、填空题(本大题共4小题,每小题5分,满分20分)
11.(5分)因式分解a2﹣b2﹣c2﹣2bc=.
12.(5分)去年年末,小王按照分期付款的方式购买一辆小轿车,总价为67.5万元,小王先首付26.5万元,以后每年还汽车销售商2万元和余款的利息,同时约定每年的年利率为6%.例如第1年年末他应付金额2+40×6%=4.4万元,第2年年末他应付金额2+38×6%=4.28万元,…,依次类推,直到还清余款为止.写出第n年年末(n为整数)应付金额y(万元)与n的函数关系式为.(不要求写n的取值范围)
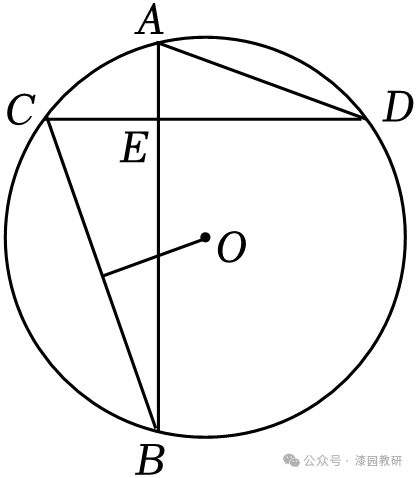
13.(5分)如图,AB、CD为⊙O的两条弦,AB⊥CD于E,OH⊥BC于H,已知AD=4,BC=6,则⊙O的半径为.
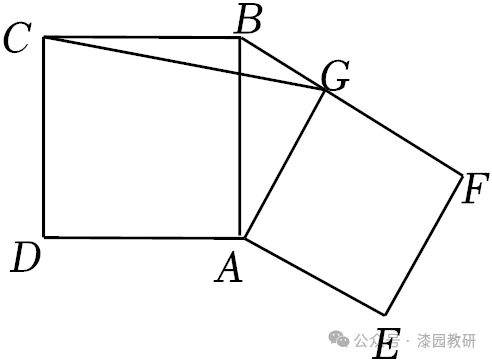
14.(5分)如图,在正方形ABCD和正方形AEFG中,AB=5,AE=4,将正方形AEFG绕点A旋转,连接CG,当∠ABG最大时,则CG的长为.
三、(本大题共2小题,每小题8分,满分16分)
15.(8分)已知关于x的一元一次不等式组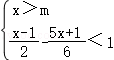 的解集为x>﹣5,求m的取值范围.
的解集为x>﹣5,求m的取值范围.
16.(8分)某专卖店销售一种工业设备,3月份的售价2万元/台,共销售60台.根据市场销售经验知:当这种设备售价每增加0.1万元/台时,每月就会少售出1台.4月份该专卖店想将销售额提高25%,这种设备售价应定价为多少万元/台?
四、(本大题共2小题,每小题8分,满分16分)
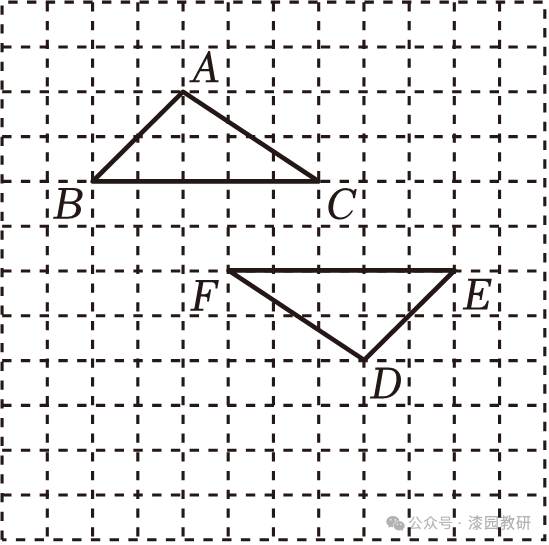
17.(8分)如图,在边长为1个单位长度的小正方形组成的网格中,给出了两个格点△ABC和△DEF(顶点是网格线的交点),已知△ABC和△DEF成中心对称.
(1)在图中找出对称中心O,并示意过程;
(2)将△DEF经过怎样平移,可与△ABC组成平行四边形?在正方形网格中画出能组成的平行四边形.
18.(8分)在“书香社区”全民阅读活动中,某社区读书联盟计划举行一次参加活动有奖送书活动,活动规则是:在一个装有2个红球和3个白球(每个球除颜色外,其它都相同) 的不透明盒中,请每位参加活动的社区居民随机摸球一次,然后送书.联盟做了三种活动计划.计划1:随机摸一个球,摸到红球送一本精美图书;计划2:随机同时摸两个球,同时摸到2个都是红球送一本精美图书;计划3:随机同时摸两个球,摸到的两个球中,其中只要有一个是红球送一本精美图书.
(1)分别求活动计划1和活动计划2中,居民获得精美图书的概率;
(2)三种活动计划中,哪种计划送出的精美图书最多?为什么?
五、(本大题共2小题,每小题10分,满分20分)
19.(10分)已知一次函数y1=ax+b与反比例函数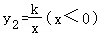 的图象相交于A(﹣1,6)、B(﹣3,2)两点.
的图象相交于A(﹣1,6)、B(﹣3,2)两点.
(1)当x<0时,比较y1与y2的大小;
(2)在y轴上找一点P,使得△PAB的周长最小,求点P的坐标.
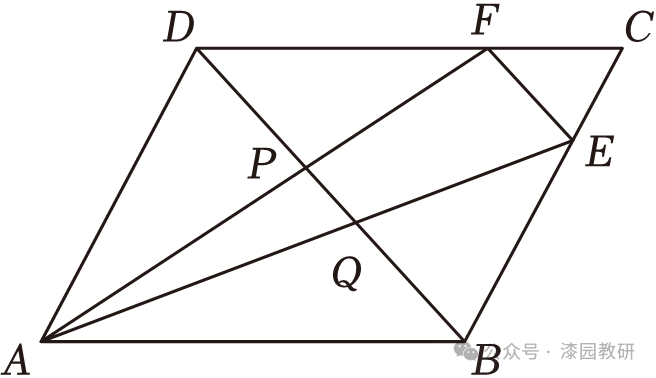
20.(10分)如图,在平行四边形ABCD中,E、F两点分别在BC、CD边上,EF∥BD,连接AFAE,分别交BD于P,Q两点.
(1)求证:S△ABE=S△ADF;
(2)求证:BQ=DP.
六、(本题满分12分)
21.(12分)关于x的一次函数y=kx+b(k,b为常数,且k≠0).
(1)若其图象经过(﹣1,m),(m,1)两点,且m>1,试判断该函数图象所经过的象限;
(2)若b=2k+3,对于任意实数k,其图象都经过定点P,求点P的坐标.
七、(本题满分12分)
22.(12分)已知关于x的二次函数y=a(x﹣m)2﹣a(x﹣m)(a,m为常数,且a≠0).
(1)若该二次函数图象的顶点M(2,3),求a,m的值;
(2)设该函数的图象与x轴交于A、B两点,与y轴交于点N,Q为函数图象的顶点.当△ABQ的面积与△ABN的面积相等时,求m的值.
八、(本题满分14分)
23.(14分)四边形ABCD内接于⊙O,AB=AD,对角线AC、BD相交于E点.
(1)如图1,点F为AC上一点,∠BFC=2∠CFD=∠BAD.
①求证:△ABF∽△DBC;
②求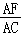 的值.
的值.
(2)如图2,求证: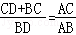 .
.
2020年安徽省芜湖市无为中学自主招生数学试卷
参考答案与试题解析
一、选择题,每小题都给出代号为A、B、C、D的四个选项,其中只有一个是正确的,请把正确选项的代号写在题后的括号内,每一小题,选对得4分,不选、选错或选出的代号超过一个的(不论是否写在括号内)一律得0分。
1.(4分)在2﹣3,,(﹣2)﹣3,这四个数中,最小的是( )
A.2﹣3B.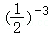 C.(﹣2)﹣3D.
C.(﹣2)﹣3D.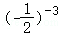
【解答】解:2﹣3=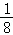 =8,(﹣2)﹣3=﹣
=8,(﹣2)﹣3=﹣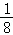 =﹣8,
=﹣8,
∵﹣8<﹣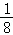 <
<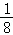 <8,
<8,
∴在2﹣3,,(﹣2)﹣3,这四个数中,最小的是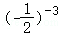
故选:D.
2.(4分)在新冠疫情阻击战中,我国有400万名社区工作者默默无闻地奋战在几十万个社区.将400万用科学记数法表示为( )
A.4×105B.4×106C.4×107D.4×108
【解答】解:400万可表示为400×10000=4×106.
故选:B.
3.(4分)下列几何体的左视图是矩形的是( )
A. B.
B. C.
C. D.
D.
【解答】解:A选项中的几何体的左视图是长方形,
B选项中的几何体的左视图是三角形,
C选项中的几何体的左视图是圆,
D选项中的几何体的左视图是梯形,
故选:A.
4.(4分)某校对180名初中毕业生进行了一次视力抽样调查,绘制出频数分布直方图(不完整)如图所示,设这次抽样调查所得数据的中位数为x,根据图中的信息判断x的取值范围是( )

A.0≤x<4.3B.4.3≤x<4.6C.4.6≤x<4.9D.4.9≤x<5.2
【解答】解:由图可知,第一组有50人,第二组有50人,
∵被调查的学生总人数是180,
∴将这180名初中毕业生进行抽样调查所得数据按从小到大的顺序排列,第90和91个数据的平均数为这组数据的中位数,
∵第90和91个数据均落在第二组,
∴这次抽样调查所得数据的中位数4.3≤x<4.6.
故选:B.
5.(4分)我国古代数学的许多创新和发展都位居世界前列,如南宋数学家杨辉(约13世纪)所著的《详解九章算术》一书中,用如图的三角形解释二项式和(a+b)n的展开式的各项系数,此三角形称为“杨辉三角”,若“杨辉三角”中第n行的各数之和比上一行各数之和大64,则n的值为( )

A.7B.8C.9D.10
【解答】解:第1行的各数之和为20,
第2行的各数之和为21,
第3行的各数之和为22,
第4行的各数之和为23,
••••••,
第n行的各数之和为2n﹣1,
∵第n行的各数之和比上一行各数之和大64,
∴2n﹣1﹣2n﹣2=64,
解得:n=8.
故选:B.
6.(4分)新定义一种运算“⊗”,其运算法则为:a⊗b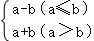 ;例如:1⊗2=﹣1,2⊗1=3.已知a⊗(﹣5)=2,则a的值为( )
;例如:1⊗2=﹣1,2⊗1=3.已知a⊗(﹣5)=2,则a的值为( )
A.3B.﹣3C.7D.﹣7
【解答】解:当a≤﹣5时,a﹣(﹣5)=2,
解得a=﹣3(不符合题意,舍去);
当a>﹣5时,a+(﹣5)=2,
解得a=7;
故选:C.
7.(4分)已知关于x的一元二次方程(a﹣b)x2+(c﹣a)x+(b﹣c)=0有两个相等的实数根且实数a,b,c互不相等,则下列结论一定成立的是( )
A.2a=b+cB.2b=a+cC.2c=a+bD.b2﹣4ac=0
【解答】解:∵关于x的一元二次方程(a﹣b)x2+(c﹣a)x+(b﹣c)=0有两个相等的实数根,
∴Δ=(c﹣a)2﹣4(b﹣c)(a﹣b)=0,
∴c2﹣2ac+a2﹣4(ab﹣b2﹣ac+bc)=0,
∴a2+4b2+c2﹣4ab+2ac﹣4bc=0,
∴(a﹣2b+c)2=0,
∴a﹣2b+c=0,
∴2b=a+c(a≠b).
故选:B.
8.(4分)已知x>0,且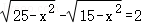 ,则与x最接近的整数是( )
,则与x最接近的整数是( )
A.4B.3C.2D.1
【解答】解:将方程两边同乘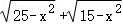 得,
得,
25﹣x2﹣(15﹣x2)=2(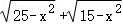 ),
),
得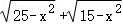 =5,
=5,
∵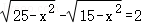
∴2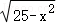 =7,
=7,
∴x=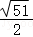 (负值已舍),
(负值已舍),
∵7< <7.5,
<7.5,
∴3.5<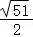 <3.75,
<3.75,
∴与x最接近的整数是4,
故选:A.
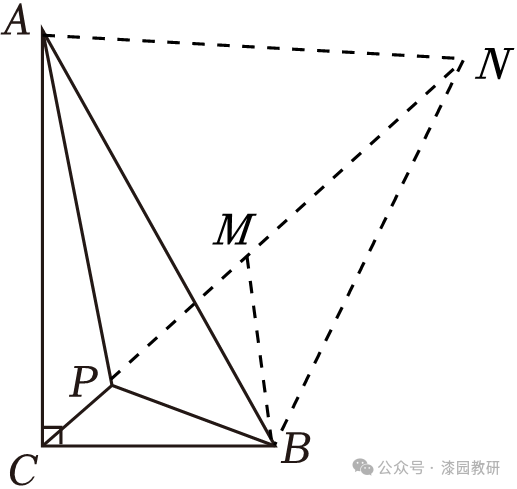
9.(4分)如图,在△ABC中,∠ACB=90°,∠BAC=30°,BC=1,P为△ABC内一点,分别连接PA、PB、PC.当∠APB=∠BPC=∠APC时,PA+PB+PC的值为( )

A.2B.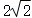 C.
C.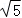 D.
D.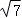
【解答】解:将△APB绕点B顺时针旋转60°到△NMB,
得△PMB,△BAN都是等边三角形,
由∠APB=∠BPC=∠APC,
得∠APB=∠BPC=∠APC=360÷3=120°,
得C,P,M,N在一直线上,
由∠ACB=90°,∠BAC=30°,BC=1,
得∠CAN=30+60=90°,AN=AB=2,AC=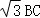 =
=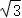
得PA+PB+PC=CN=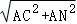 =
=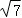 .
.
故选:D.
10.(4分)如图,在△ABC中,CD⊥AB于D,AD=9,DB=3,CD=6,矩形的顶点E与A点重合,EF=8,EH=4,将矩形EFGH沿AB平移,当点E与点B重合时,停止平移,设点E平移的距离为x,矩形EFGH与△ABC重合部分的面积为y,则y关于x的函数图象大致为( )

A. B.
B.
C. D.
D.
【解答】解:当0<x≤4时,设AC,EF交于点I,如图,
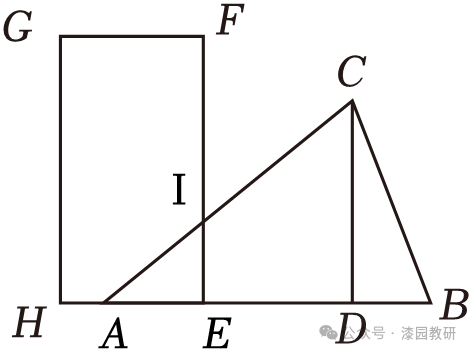
∵IE∥CD,
∴△AIE∽△ACD,
∴IE:CD=AE:AD,即IE:6=x:9,
∴IE=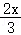
∴y=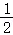 x•
x•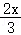 =
=
当4<x≤9时,设GH交AC于点J,如图,
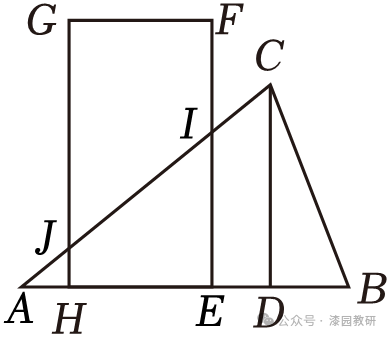
∵△AJH∽△ACD,
∴AH:AD=JH:CD,
∵HE=4,∴AH=x﹣4,
∴(x﹣4):9=JH:6,
∴JH=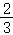 (x﹣4),
(x﹣4),
∴y=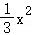 ﹣
﹣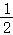 (x﹣4)•
(x﹣4)•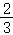 (x﹣4)=
(x﹣4)=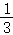 (x﹣4)2=
(x﹣4)2=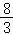 x﹣
x﹣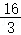
当9<x≤12时,设BC,EF交于点I,如图,
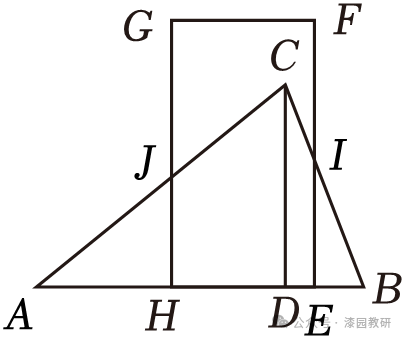
∵IE∥CD,
∴△BIE∽△BCD,
∴IE:CD=BE:BD,
∵AB=12,
∴BE=12﹣x,IE=24﹣2x,
∵AH=x﹣4,
∴HD=9﹣(x﹣4)=13﹣x,DE=x﹣9,
∴y=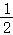 [
[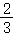 (x﹣4)+6](13﹣x)+
(x﹣4)+6](13﹣x)+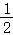 (24﹣2x+6)(x﹣9)=﹣
(24﹣2x+6)(x﹣9)=﹣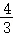 x2+30x﹣
x2+30x﹣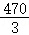 ;
;
由这三段函数可以判断C符合题意,
故选:C.
二、填空题(本大题共4小题,每小题5分,满分20分)
11.(5分)因式分解a2﹣b2﹣c2﹣2bc=(a+b+c)(a﹣b﹣c).
【解答】解:a2﹣b2﹣c2﹣2bc=a2﹣(b2+2bc+c2)=a2﹣(b+c)2=(a+b+c)(a﹣b﹣c),
故答案为:(a+b+c)(a﹣b﹣c).
12.(5分)去年年末,小王按照分期付款的方式购买一辆小轿车,总价为67.5万元,小王先首付26.5万元,以后每年还汽车销售商2万元和余款的利息,同时约定每年的年利率为6%.例如第1年年末他应付金额2+40×6%=4.4万元,第2年年末他应付金额2+38×6%=4.28万元,…,依次类推,直到还清余款为止.写出第n年年末(n为整数)应付金额y(万元)与n的函数关系式为y=﹣0.12n+4.52.(不要求写n的取值范围)
【解答】解:设第n年年末(n为整数)应付金额y(万元)与n的函数关系式为y=kn+b(k≠0),
将(1,4.4),(2,4.28)代入y=kn+b得: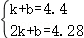
解得: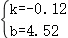
∴第n年年末(n为整数)应付金额y(万元)与n的函数关系式为y=﹣0.12n+4.52.
故答案为:y=﹣0.12n+4.52.
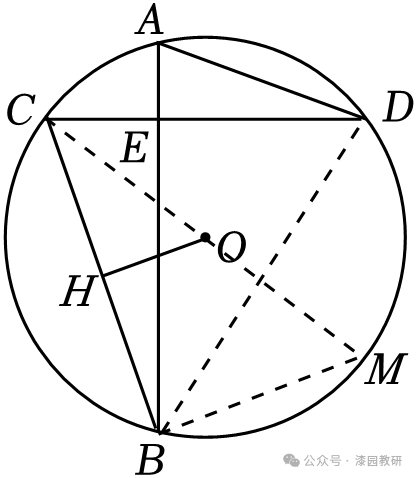
13.(5分)如图,AB、CD为⊙O的两条弦,AB⊥CD于E,OH⊥BC于H,已知AD=4,BC=6,则⊙O的半径为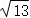 .
.

【解答】解:作直径CM,连接MB,BD,
∴∠CBM=90°,
∴∠BCM+∠M=90°,
∵AB⊥CD⊥,
∴∠BED=90°,
∴∠ABD+∠BDE=90°,
∵∠M=∠BDE,
∴∠BCM=∠ABD,
∴ =
=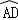
∴MB=AD=4,
∵BC=6,
∴CM=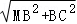 =2
=2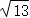
∴⊙O的半径为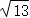 .
.
故答案为: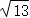 .
.
14.(5分)如图,在正方形ABCD和正方形AEFG中,AB=5,AE=4,将正方形AEFG绕点A旋转,连接CG,当∠ABG最大时,则CG的长为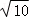 或
或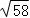 .
.

【解答】解:由题意可知,点G的运动轨迹是以A为圆心,AG为半径的圆,当BG与⊙A相切时,∠ABG的值最大;
当点G在AB右侧时,如图,过点G作GM⊥CB交CB的延长线于点M,过点G作GN⊥AB于点N,
易证四边形BNGM为矩形,
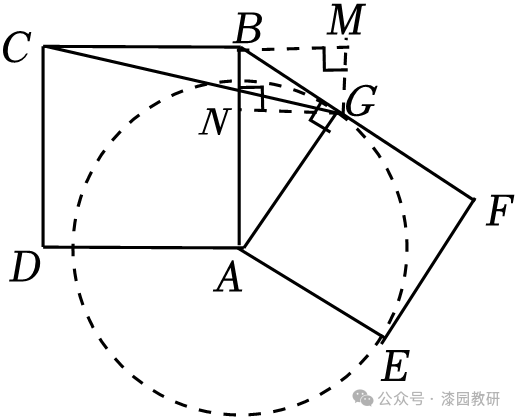
在正方形ABCD中,AB=BC.
∵BG是⊙A的切线,
∴AG⊥BG,
∵AB=5,AG=4,
∴BG=3,
∵∠GAN=∠BAG,∠AGB=∠ANG,
∴△ABG∽△AGN,
∴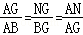
∴NG=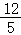 =
=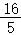
∴MG=BN=AB﹣AN=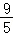 =CB+BM=AB+NG=5+
=CB+BM=AB+NG=5+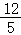 =
=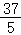
∴CG=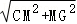 =
=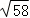 ;
;
当点G在AB左侧时,如图,过点G作GM⊥CD于点M,过点G作GN⊥AB于点N,
∵四边形ABCD是正方形,
∴四边形BNMC为矩形,
∵BG是⊙A的切线,
∴AG⊥BG,
∵AB=5,AG=4,
∴BG=3,
∵∠GAN=∠BAG,∠AGB=∠ANG,
∴△ABG∽△AGN,
∴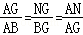
∴NG=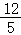 =
=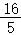
∴MG=MN﹣NG=BC﹣NG=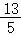 =CD﹣DM=AB﹣AN=5﹣
=CD﹣DM=AB﹣AN=5﹣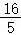 =
=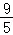
∴CG=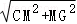 =
=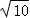 ;
;
则答案为: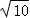 或
或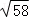 .
.


三、(本大题共2小题,每小题8分,满分16分)
15.(8分)已知关于x的一元一次不等式组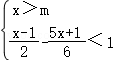 的解集为x>﹣5,求m的取值范围.
的解集为x>﹣5,求m的取值范围.
【解答】解:由题意,∵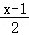 ﹣
﹣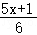 <1,
<1,
∴3(x﹣1)﹣(5x+1)<6,
3x﹣3﹣5x﹣1<6,
∴﹣2x<10.
∴x>﹣5.
又x>m,且不等式组的解集我x>﹣5,
∴m≤﹣5.
16.(8分)某专卖店销售一种工业设备,3月份的售价2万元/台,共销售60台.根据市场销售经验知:当这种设备售价每增加0.1万元/台时,每月就会少售出1台.4月份该专卖店想将销售额提高25%,这种设备售价应定价为多少万元/台?
【解答】解:设这种设备售价应定价为x万元/台,
由题意得:x(60﹣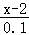 )=2×60×(1+25%),
)=2×60×(1+25%),
整理得:x2﹣8x+15=0,
解得:x1=3,x2=5,
答:这种设备售价应定价为3万元/台或5万元/台.
四、(本大题共2小题,每小题8分,满分16分)
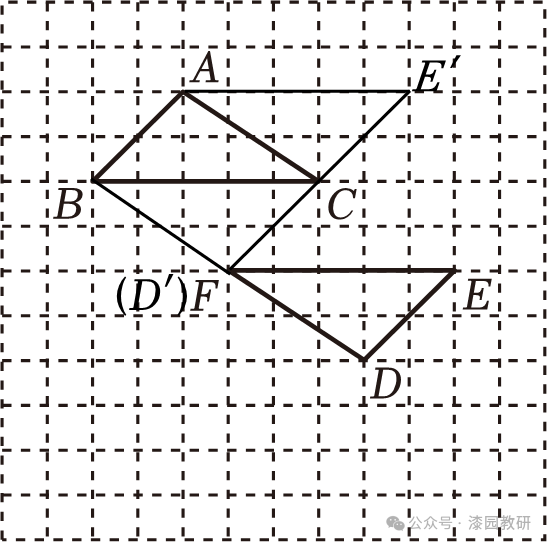
17.(8分)如图,在边长为1个单位长度的小正方形组成的网格中,给出了两个格点△ABC和△DEF(顶点是网格线的交点),已知△ABC和△DEF成中心对称.
(1)在图中找出对称中心O,并示意过程;
(2)将△DEF经过怎样平移,可与△ABC组成平行四边形?在正方形网格中画出能组成的平行四边形.

【解答】解:(1)如图,连接AD,BE,CF,相交于点O,
则△ABC和△DEF关于点O成中心对称,
则点O即为所求.
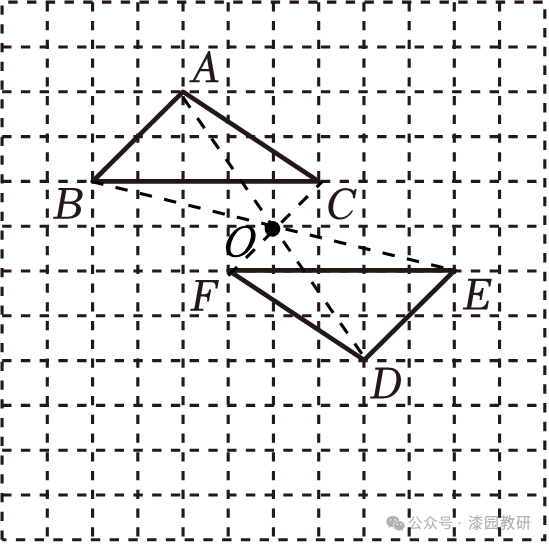
(2)如图,将△DEF向左平移3个单位长度,向上平移2个单位长度,可与△ABC组成平行四边形ABD'C.
将△DEF向左平移1个单位长度,向上平移4个单位长度,可与△ABC组成平行四边形ABCE'.
18.(8分)在“书香社区”全民阅读活动中,某社区读书联盟计划举行一次参加活动有奖送书活动,活动规则是:在一个装有2个红球和3个白球(每个球除颜色外,其它都相同) 的不透明盒中,请每位参加活动的社区居民随机摸球一次,然后送书.联盟做了三种活动计划.计划1:随机摸一个球,摸到红球送一本精美图书;计划2:随机同时摸两个球,同时摸到2个都是红球送一本精美图书;计划3:随机同时摸两个球,摸到的两个球中,其中只要有一个是红球送一本精美图书.
(1)分别求活动计划1和活动计划2中,居民获得精美图书的概率;
(2)三种活动计划中,哪种计划送出的精美图书最多?为什么?
【解答】解:(1)活动计划1:共有5种等可能的结果,其中摸到红球的结果有2种,
∴居民获得精美图书的概率为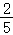 .
.
活动计划2:列表如下:
红 | 红 | 白 | 白 | 白 | |
红 | (红,红) | (红,白) | (红,白) | (红,白) | |
红 | (红,红) | (红,白) | (红,白) | (红,白) | |
白 | (白,红) | (白,红) | (白,白) | (白,白) | |
白 | (白,红) | (白,红) | (白,白) | (白,白) | |
白 | (白,红) | (白,红) | (白,白) | (白,白) |
共有20种等可能的结果,其中同时摸到2个都是红球的结果有2种,
∴居民获得精美图书的概率为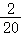 =
=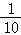 .
.
(2)活动计划3:列表如下:
红 | 红 | 白 | 白 | 白 | |
红 | (红,红) | (红,白) | (红,白) | (红,白) | |
红 | (红,红) | (红,白) | (红,白) | (红,白) | |
白 | (白,红) | (白,红) | (白,白) | (白,白) | |
白 | (白,红) | (白,红) | (白,白) | (白,白) | |
白 | (白,红) | (白,红) | (白,白) | (白,白) |
共有20种等可能的结果,其中至少有一个是红球的结果有14种,
∴居民获得精美图书的概率为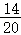 =
=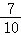 .
.
∵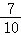 >
>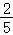 >
>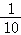
∴活动计划3送出的精美图书最多.
五、(本大题共2小题,每小题10分,满分20分)
19.(10分)已知一次函数y1=ax+b与反比例函数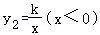 的图象相交于A(﹣1,6)、B(﹣3,2)两点.
的图象相交于A(﹣1,6)、B(﹣3,2)两点.
(1)当x<0时,比较y1与y2的大小;
(2)在y轴上找一点P,使得△PAB的周长最小,求点P的坐标.
【解答】解:(1)∵一次函数y1=ax+b过A(﹣1,6)、B(﹣3,2),
∴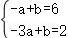
解得a=2,b=8,
∴一次函数的关系式为y1=2x+8,
∵反比例函数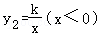 的图象过A(﹣1,6),
的图象过A(﹣1,6),
∴k=﹣1×6=﹣6,
∴反比例函数的关系式为y2=﹣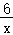
两个函数的图象如图所示,由图象可知,
当x<﹣3或﹣1<x<0时,y2>y1,
当﹣3<x<﹣1时,y1>y2;
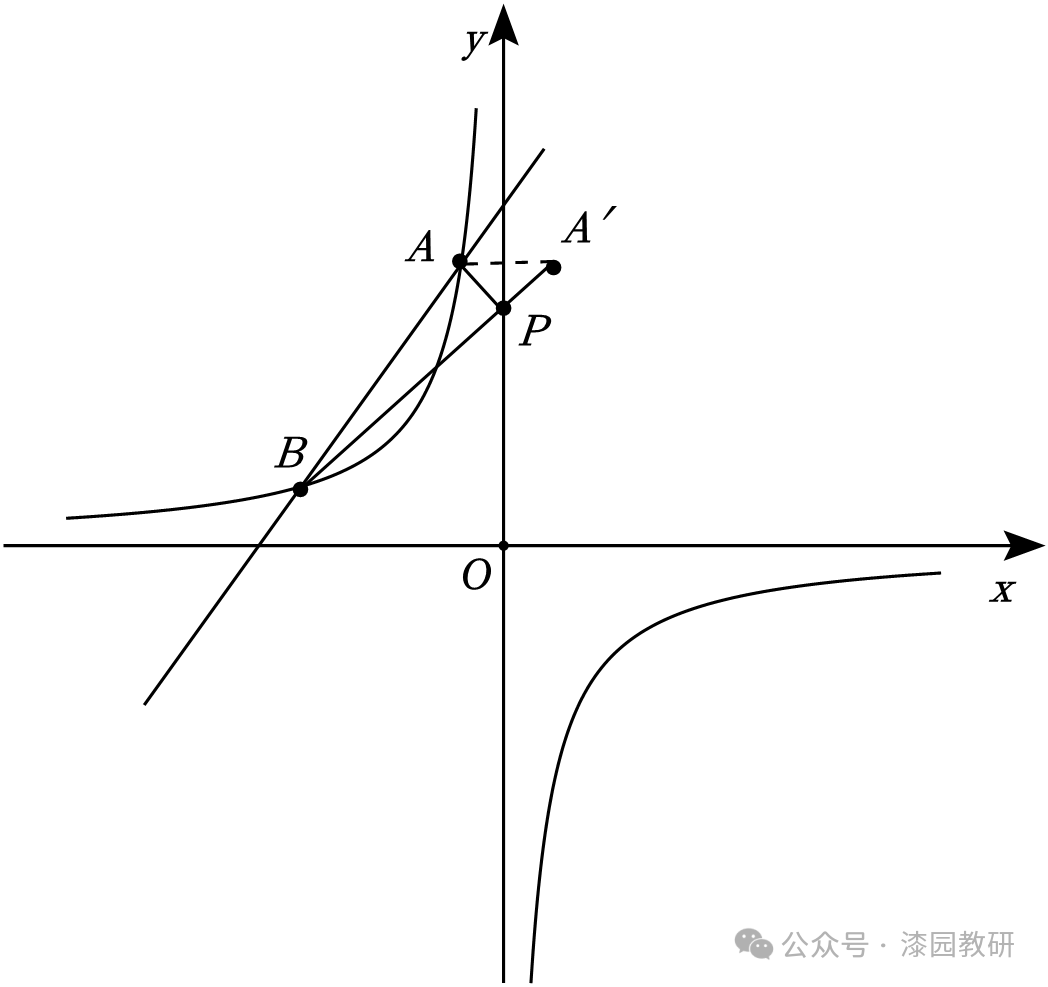
(2)如图,作点A(﹣1,6)关于y轴对称点A′,则A′(1,6),
设直线BA′的关系式为y=mx+n,则
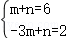
解得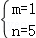
∴直线BA′的关系式为y=x+5,
当x=0时,y=5,
∴点P(0,5),此时△PAB的周长最小.
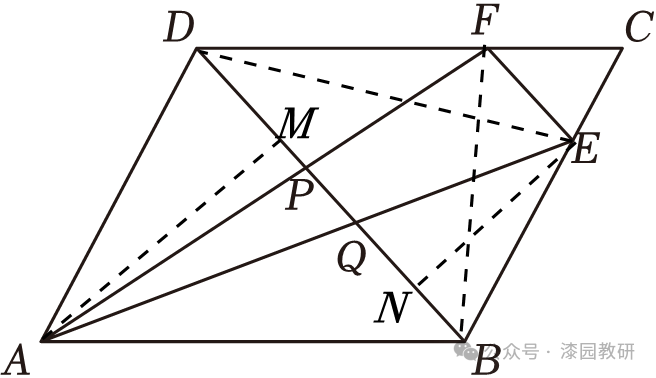
20.(10分)如图,在平行四边形ABCD中,E、F两点分别在BC、CD边上,EF∥BD,连接AFAE,分别交BD于P,Q两点.
(1)求证:S△ABE=S△ADF;
(2)求证:BQ=DP.

【解答】证明:(1)连接DE,BF,
∵FE∥BD,
∴△DFB的面积=△BDE的面积,
∵四边形ABCD是平行四边形,
∴AD∥BC,CD∥AB,
∴△ABE的面积=△BDE的面积,△ADF的面积=△DFB的面积,
∴S△ABE=S△ADF;
(2)过A作AM⊥BD于M,过E作EN⊥BD于N,
∵△ADF的面积=△ABE的面积,
∴△ADP的面积+△PDF的面积=△ABQ的面积+△BEQ的面积,
∴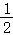 PD•AM
PD•AM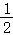 PD•EN=
PD•EN=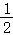 BQ•AM+
BQ•AM+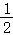 BQ•EN,
BQ•EN,
∴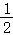 PD•(AM+EN)=
PD•(AM+EN)=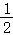 BQ•(AM+EN),
BQ•(AM+EN),
∴PD=BQ.
六、(本题满分12分)
21.(12分)关于x的一次函数y=kx+b(k,b为常数,且k≠0).
(1)若其图象经过(﹣1,m),(m,1)两点,且m>1,试判断该函数图象所经过的象限;
(2)若b=2k+3,对于任意实数k,其图象都经过定点P,求点P的坐标.
【解答】解:(1)∵一次函数y=kx+b的图象经过(﹣1,m),(m,1)两点,
∴﹣k+b=m,mk+b=1,解得:k=(1﹣m)/(m+1),b=(m2+1)/(m+1),
∵m>1,
∴1﹣m<0,m+1>0,m2+1>0,
∴k<0,b>0,
∴该函数的图形经过第一、二、四象限;
(2)∵b=2k+3,
∴y=kx+b=kx+2k+3
即y=k(x+2)+3,
对于任意实数k,都有当x=﹣2时,y=3,
∴对于任意实数k,其图象都经过定点(﹣2,3),
故点P的坐标为(﹣2,3).
七、(本题满分12分)
22.(12分)已知关于x的二次函数y=a(x﹣m)2﹣a(x﹣m)(a,m为常数,且a≠0).
(1)若该二次函数图象的顶点M(2,3),求a,m的值;
(2)设该函数的图象与x轴交于A、B两点,与y轴交于点N,Q为函数图象的顶点.当△ABQ的面积与△ABN的面积相等时,求m的值.
【解答】解:(1)由题意,∵y=a(x﹣m)2﹣a(x﹣m)=a[(x﹣m)2﹣(x﹣m)+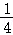 ]﹣
]﹣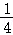 a=a(x﹣m﹣
a=a(x﹣m﹣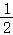 )2﹣
)2﹣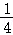 a,
a,
∴顶点为(m+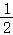 ,﹣
,﹣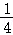 a).
a).
又顶点M(2,3),
∴m+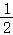 =2,﹣
=2,﹣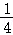 a=3.
a=3.
∴a=﹣12,m=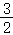 .
.
(2)由题意,当x=0时,y=a(0﹣m)2﹣a(0﹣m)=am2+am,
∴点N的坐标为(0,am2+am).
又令y=0,
∴a(x﹣m)2﹣a(x﹣m)=a(x﹣m)(x﹣m﹣1)=0.
∴x1=m,x2=m+1.
∴AB=(m+1)﹣m=1.
∴△ABN的面积=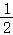 ×1×|am2+am|.
×1×|am2+am|.
又y=a(x﹣m)2﹣a(x﹣m)=a(x﹣m﹣ )2﹣
)2﹣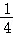 a,
a,
∴△ABQ的面积=×1×|﹣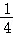 a|.
a|.
∵△ABQ的面积与△ABN的面积相等,
∴ ×1×|am2+am|=×1×|﹣
×1×|am2+am|=×1×|﹣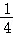 a|.
a|.
整理得,m2+m﹣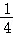 =0或m2+m+
=0或m2+m+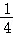 =0,
=0,
解得m=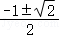 或m=﹣
或m=﹣ .
.
八、(本题满分14分)
23.(14分)四边形ABCD内接于⊙O,AB=AD,对角线AC、BD相交于E点.
(1)如图1,点F为AC上一点,∠BFC=2∠CFD=∠BAD.
①求证:△ABF∽△DBC;
②求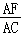 的值.
的值.
(2)如图2,求证: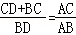 .
.

【解答】(1)①证明:∵AB=AD,
∴∠ABD=∠ADB,
∵∠BFC=∠BAC+∠ABF,∠BFC=∠BAD=∠BAC+∠CAD,
∴∠DAC=∠ABF,
∵∠DBC=∠CAD,
∴∠ABF=∠DBC,
∵∠BAF=∠BDC,
∴△ABF∽△DBC;
②解:作∠BFC的角平分线交BC于点G,
则∠CFG=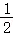 ∠BFC=∠CFD,
∠BFC=∠CFD,
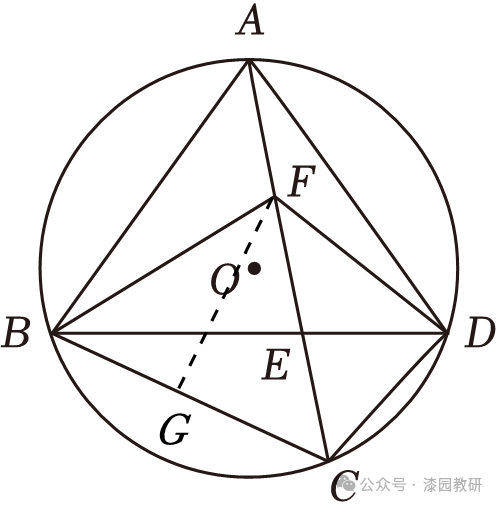
∵AB=AD,
∴∠ACB=∠ACD,
∵CF=CF,
∴△FCG≌△FCD(ASA),
∴CG=CD,
∵∠CBD=∠ABF,
∴∠ABD=∠FBC=∠ACD=∠ACB,
∴FB=FC,
∴FG垂直平分BC,
∴CG=BG=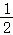 BC=CD,
BC=CD,
∴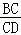 =2,
=2,
∵△ABF∽△DBC,
∴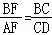 =2,
=2,
∴BF=2AF=CF,
∴AC=AF+CF=3AF,
∴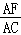 =
=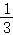 .
.
(2)证明:在AC上截取点F,使∠ABF=∠CBD,连接BF,
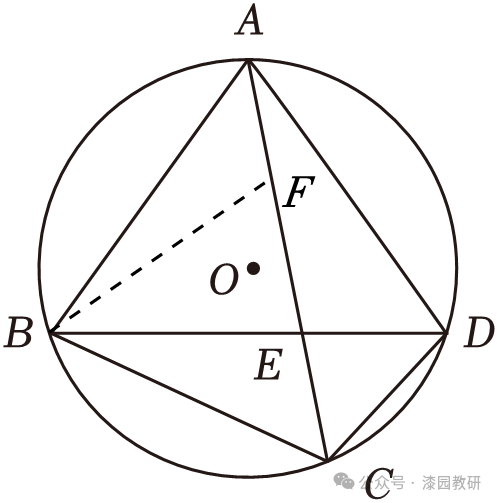
由(1)①知△ABF∽△DBC,
∴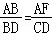
∴AF•BD=AB•CD...①
由(1)②知∠ABD=∠FBC=∠ACD=∠ACB=∠ADB,
∴△FBC∽△ABD,
∴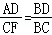
∴BD•CF=AD•BC...②
①+②得,AF•BD+BD•CF=AB•CD+AD•BC,
∵AB=AD,
∴BD•(AF+CF)=AB•(CD+BC),
即BD•AC=AB•(CD+BC),
∴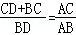 .
.
声明:试题解析著作权属菁优网所有,未经书面同意,不得复制发布日期:2024/7/14 22:29:21;用户:mczl58;邮箱:ldwh135@xyh.com;学号:24737059
本文由小编发布,不代表一本线高考网立场,转载联系作者并注明出处:https://www.yibenxian.com/tiku/57204.html

