电场磁场电磁感应近代物理必记规律结论
电场
1.两个定律
(1)电荷守恒定律:电荷既不会创生,也不会消灭,它只能从一个物体转移到另一个物体,或者从物体的一部分转移到另一部分;在转移过程中,电荷的总量保持不变。
(2)库仑定律
①=k ,r指两点电荷间的距离。对可视为点电荷的两个均匀带电球,r为两球心间距。
,r指两点电荷间的距离。对可视为点电荷的两个均匀带电球,r为两球心间距。
②当两个电荷间的距离r→0时,电荷不能视为点电荷,它们之间的静电力不能认为趋于无限大。
2.电场的力的性质

3.电场的能的性质
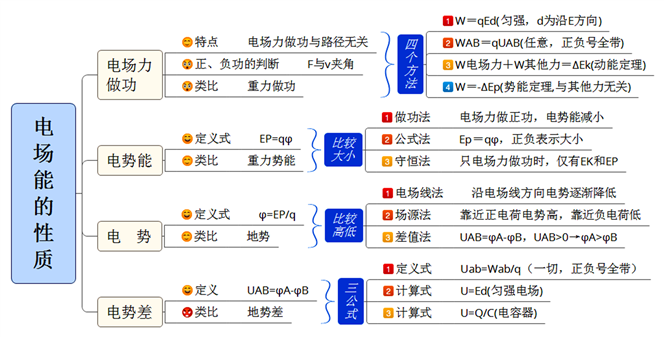
4.电势差与电场强度的关系
(1)匀强电场中电势差与场强的关系式:UAB=Ed,其中d为电场中两点间沿电场方向的距离。
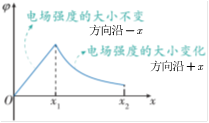
(2)电场强度的方向和大小:沿电场强度的方向电势降低最快。在匀强电场中,场强在数值上等于沿电场方向每单位距离上降低的电势。
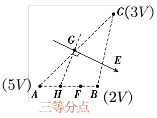
(3)已知三点电势求场强
等分法 | 平行结论法 | 正交分解法 |
|
|
|
匀强电场中同一条直线上的两段电势差正比于线段长度。 | 匀强电场中若两线段平行,则这两段电势差正比于线段长度。题中出现平行线时可用此方法。 | 匀强电场中,利用E=U/d,分别求出两垂直方向的场强,再求出合场强。只有垂直时才能用此方法。 |
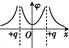
5.等量点电荷的电场电场强度与电势分布规律
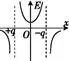
电场 | 等势面(实线) | E-x | φ-x |
等量异 号点电 荷的电 场 |
|
两电荷连线上 |
两电荷连线上 |
连线中垂线上 | 连线中垂线 上各点电势 相等且为零 | ||
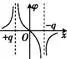
等量同 号正点 电荷的 电场 |
|
两电荷连线上 |
两电荷连线上 |
连线中垂线上 |
连线中垂线上 |
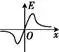
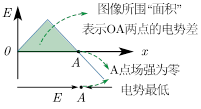
6.电场中的图像问题
φ-x图像 | E-x图像 | EP-x图像 |
|
|
|
斜率:电场强度 | 面积:电势差 | 斜率:电场力 |
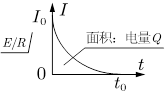
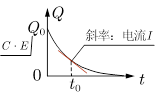
7.电容器放电过程中的I-t图、Q-t图、U-t图
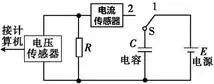
I-t图 | Q-t图 | U-t图 |
|
|
|
8.平行板电容器的动态分析方法
(1)确定不变量―→分析是电压不变还是所带电荷量不变。
(2)用决定式C=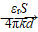 分析平行板电容器电容的变化。
分析平行板电容器电容的变化。
(3)用定义式C= ―→分析电容器所带电荷量或两极板间电压的变化。
―→分析电容器所带电荷量或两极板间电压的变化。
(4)用E=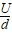 ―→分析电容器极板间电场强度的变化。
―→分析电容器极板间电场强度的变化。
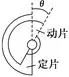
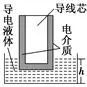
9.常见电容式传感器
|
|
|
|
测定角度θ的电容式传感器 | 测定液面高度h的电容式传感器 | 测定压力F的电容式传感器 | 测定位移x的电容式传感器 |
10.静电平衡状态
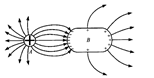
导体中(包括表面)没有电荷定向移动的状态叫做静电平衡状态。静电平衡状态下导体具有的特征总结为以下四点:
(1) 导体内部场强为零;
(2) 净电荷仅分布在导体表面上(孤立导体的净电荷仅分布在导体的外表面上);
(3) 导体为等势体,导体表面为等势面,电场线与导体表面处处垂直。
(4) 静电平衡时内部场强为零的现象,在技术上用来实现静电屏蔽。
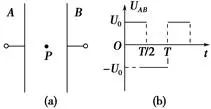
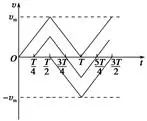
11.图像法分析带电粒子在交变电场中的运动
不计重力时,粒子在电场中运动的加速度 ,根据U-t图画出a-t图,再画出v-t图,利用图像的面积可求出位移。注意粒子开始运动的时刻不同,使得物体可能做单向直线运动,也可能做往复直线运动。
,根据U-t图画出a-t图,再画出v-t图,利用图像的面积可求出位移。注意粒子开始运动的时刻不同,使得物体可能做单向直线运动,也可能做往复直线运动。
12.电偏转

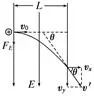
13.偏移、偏转角和动能增量
质量为m电荷量为q(不计重力)的带电粒子以平行于极板的初速度v0射入长L板间距离为d的平行板电容器间,两板间电压为U。
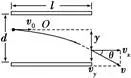

加速度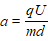 ;时间
;时间 (水平)、
(水平)、 (竖直)
(竖直)
⑴偏移: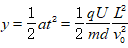 (粒子出电场);
(粒子出电场);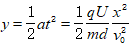 (粒子未出电场,打板)
(粒子未出电场,打板)
⑵偏角: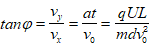 (粒子出电场);
(粒子出电场);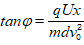 (粒子未出电场,打板)
(粒子未出电场,打板)
⑶穿越电场过程的动能增量:ΔEK=qEy(注意,一般来说不等于qU)
14.先加速后偏转
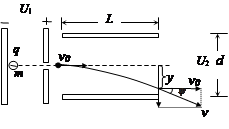
不同的带电粒子由静止开始经过同一电场(U1)加速后,再从同一偏转电场(电压U2、板宽d、板长L)射出时的偏移y、偏转角度φ总是相同的。证明:
(1)由qU1= ;
; 得
得
(2)由qU1= ;
;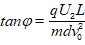 ,得tanφ=
,得tanφ=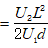 。
。
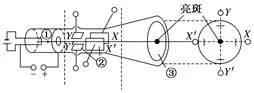
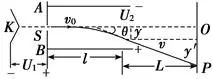
15.示波管的工作原理
在示波管模型中,带电粒子经加速电场U1加速,再经偏转电场U2偏转后,需要经历一段匀速直线运动才会打到荧光屏上而显示亮点P,如图所示.确定最终偏移:

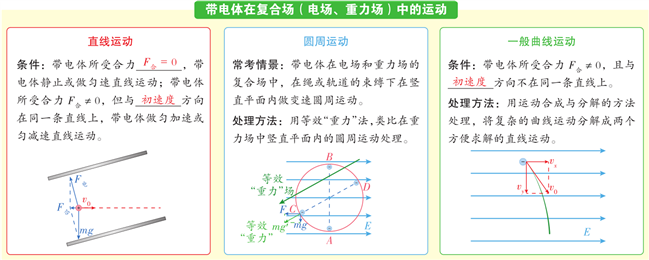
16.带电体在复合场中的运动
磁场
1.磁感应强度和磁感线
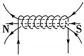
(1)电流产生的磁场方向
安培定则 |
|
|
|
立体图 |
|
|
|
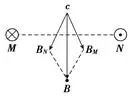
(2)磁感应强度的叠加——平行四边形法则
(3)地磁场特点
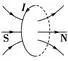
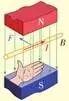
①地磁场的N极在地理南极附近,地磁场的S极在地理北极附近,磁感线分布如图所示。
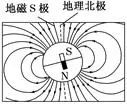
图
②地磁场B的水平分量(Bx)总是从地理南极指向地理北极,而竖直分量(By),在南半球垂直地面向上,在北半球垂直地面向下。赤道处的地磁场沿水平方向,指向北。
2.安培力
安培力公式F=BIL,要求两两垂直,应用时要满足:
(1)B与L垂直;
(2)L是有效长度,即垂直磁感应强度方向的直线长度,如弯曲导线的有效长度L等于两端点所连直线的长度(如图所示),相应的电流方向沿L由始端流向末端。
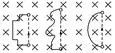
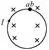
(3)安培力的方向——左手定则
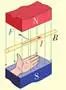
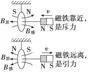
(4)两平行通电直导线的相互作用:“同流合污”

(5)安培力作用下的平衡问题,解题的关键是要根据立体图画出受力的平面图。


(6)两种电路连接方式所受安培力的区别
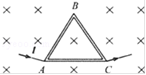
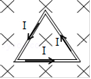
F=BI1L+BI2L=BILF=0
3.匀速圆周运动半径公式和周期公式
若v⊥B,带电粒子仅受洛伦兹力作用,在垂直于磁感线的平面内以入射速度v做匀速圆周运动.
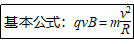 →导出公式:半径R=
→导出公式:半径R=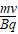 周期T=
周期T=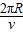 =
=
说明:
①R∝mv(动量),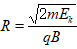
②T与速度v无关。
4..带电粒子在有界磁场中的运动
(1)圆心的确定
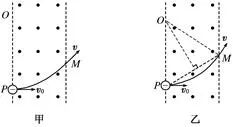
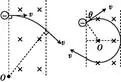
①已知入射方向和出射方向时,可通过入射点和出射点作垂直于入射方向和出射方向的直线,两条直线的交点就是圆弧轨道的圆心(如图甲所示,图中P为入射点,M为出射点)。
②已知入射方向和出射点的位置时,可以通过入射点作入射方向的垂线,连接入射点和出射点,作其中垂线,这两条垂线的交点就是圆弧轨道的圆心(如图乙所示,P为入射点,M为出射点)。
(2)半径的确定和计算
利用平面几何关系,求出该圆的可能半径(或圆心角),求解时注意以下几个重要的几何特点:
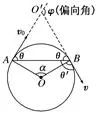
图
(1)粒子速度的偏向角(φ)等于圆心角(α),并等于AB弦与切线的夹角(弦切角θ)的2倍(如图),即φ=α=2θ=ωt。
(2)相对的弦切角(θ)相等,与相邻的弦切角(θ′)互补,即θ+θ′=180°。
(3)直角三角形的几何知识(勾股定理)。AB中点C,连接OC,则△ACO、△BCO都是直角三角形。
(3)运动时间的确定
粒子在磁场中运动一周的时间为T,当粒子运动的圆弧所对应的圆心角为α时,其运动时间可由下式表示:
t=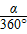 T(或t=
T(或t=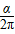 T),t=
T),t=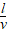 (l为弧长)。
(l为弧长)。
【巧学活用】(1)处理该类问题常用的几个几何关系
① 3个点:入射点、出射点、轨迹圆心;
② 3条线:入射点、出射点与圆心的连线——半径,入射点与出射点的连线——弦;
③ 3个角:速度偏转角、圆心角、弦切角,其中偏转角等于圆心角,也等于弦切角的两倍。
(2)带电粒子在不同边界磁场中的运动:
类别 | 特点 | 图示 |
直线 边界 | 进出磁 场具有 对称性 |
|
平行 边界 | 存在临界条件 |
|
圆形 边界 | 沿径向射 入必沿径 向射出 |
|
环形 边界 | 与边界相切 |
|
5.带电粒子在磁场中运动的临界与极值问题
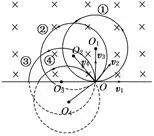
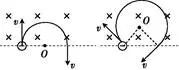
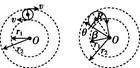
(1)动态放缩法
当带电粒子射入磁场的方向确定,但射入时的速度v大小或磁场的强弱B变化时,粒子做圆周运动的轨道半径r随之变化。在确定粒子运动的临界情景时,可以以入射点为定点,将轨道半径放缩,作出一系列的轨迹,从而探索出临界条件。如图所示,粒子进入长方形边界OABC形成的临界情景为②和④。

图
(2)定圆旋转法
当带电粒子射入磁场时的速率v大小一定,但射入的方向变化时,粒子做圆周运动的轨道半径r是确定的。在确定粒子运动的临界情景时,可以以入射点为定点,将轨迹圆旋转,作出一系列轨迹,从而探索出临界条件,如图所示为粒子进入单边界磁场时的情景。
6.运动的往复性形成多解
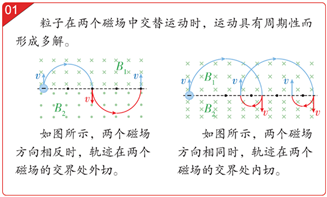

7.“磁发散”和“磁聚焦”
磁发散 | 磁聚焦 |
带电粒子从圆形有界匀强磁场边界上同一点射入,如果轨迹半径与磁场半径相等,则粒子出射方向与入射点的切线方向平行 | 带电粒子平行射入圆形有界匀强磁场,如果轨迹半径与磁场半径相等,则粒子从磁场边界上同一点射出,该点切线与入射方向平行 |
|
8.“电偏转”和“磁偏转”的比较
垂直进入磁场(磁偏转) | 垂直进入电场(电偏转) | |
情景图 |
|
|
受力 | FB=qv0B大小不变,方向总指向圆心,方向变化,FB为变力 | FE=qE,FE大小、方向不变,为恒力 |
运动规律 | 匀速圆周运动 r= | 类平抛运动 vx=v0,vy= x=v0t,y= |
运动时间 | t= | t= |
动能 | 不变 | 变化 |
9.弦长公式
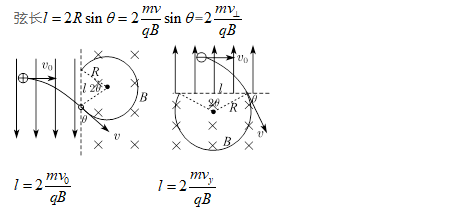
10.带电粒子在复合场中的两类典型运动
匀速直线运动 | 匀速圆周运动 |
|
|
11.带电粒子在叠加场中运动的实例分析

恒定电流
1.三个定律
(1)欧姆定律(部分电路)
①伏安特性曲线
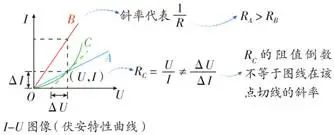
②电流的三个表达式:(i)I= (定义式);(ii)
(定义式);(ii) (决定式,欧姆定律);(iii)I=neSv(微观决定式)
(决定式,欧姆定律);(iii)I=neSv(微观决定式)
(2)电阻定律
表达式:R=ρ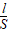 (决定式);电阻定义式:R=
(决定式);电阻定义式:R=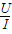 。
。
(3)焦耳定律
(1)电功和电热
①电功:W=qU=UIt。
②电热:电流流过一段导体时产生的热量Q=I2Rt(焦耳定律)。
③纯电阻电路与非纯电阻电路对比
纯电阻电路 | 非纯电阻电路 | |
实例 | 白炽灯、电炉、电饭锅、电热毯、电熨斗及转子被卡住的电动机等 | 电动机、电解槽、日光灯等 |
电功与电热 | W=UIt,Q=I2Rt= | W=UIt,Q=I2Rt,W>Q |
2.闭合电路欧姆定律
(1)路端电压U与电流I的关系:U=E-Ir.

①当电路断路即I=0时,纵坐标的截距为电源电动势.
②当外电路短路即U=0时,横坐标的截距为短路电流.
③图线的斜率的绝对值为电源的内阻.
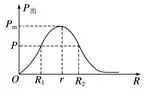
(2)纯电阻电路中输出功率随R的变化关系:P出=I2R=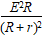
①当R=r时,电源的输出功率最大为Pm=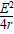 .
.
②当P出<Pm时,每个输出功率对应两个外电阻R1和R2,且R1R2=r2.
3.含电容器电路的分析
(1)电路的简化“先去后并”:不分析电容器的充、放电过程时,把电容器所处的支路视为断路,简化电路时可以去掉,求电荷量时再在相应位置补上.
(2)处理方法:电路稳定后,与电容器串联的电路中没有电流,同支路的电阻相当于导线,即电阻不起降低电压的作用,与电容器串联的电阻视为等势体.电容器的电压为与之并联的电阻两端的电压.
(3)电容器所带电荷量的变化的计算:
①如果变化前后极板带电的电性相同,那么通过所连导线的电荷量等于初、末状态电容器所带电荷量之差;
②如果变化前后极板带电的电性相反,那么通过所连导线的电荷量等于初、末状态电容器所带电荷量之和.
4.电路的动态分析常用方法:
(1)程序法:电路结构的变化(电阻变化)→总电阻的变化→总电流的变化→路端电压的变化→固定支路电压、电流的分析→变化支路电压、电流的分析。
(2)极限法:因滑动变阻器滑片滑动引起的电路变化问题,可将滑动变阻器的滑动端分别滑至两个极端去讨论。
(3)串反并同:当电路中电阻变化时,与变化电阻成串联关系的用电器的电流变化情况与电阻变化情况相反,与变化电阻成并联关系的用电器的电流变化情况与电阻变化情况相同。
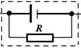
5.两类等效电源
等效电源法 | 第一类: | 第二类: |
等效电动势 |
|
|
等效内阻 |
|
|
6.U/I和ΔU/ΔI区别
(1)对于定值电阻R:R= =
=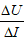 ;
;
(2)对于可变电阻:R= ≠
≠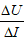 ;
;
(3)等效电源的内阻:电路的动态分析中,等效电源的内阻等于路端电压的变化量U与干路电流的变化量ΔI的比值的绝对值,即r=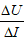 .
.
电磁感应
1.判断感应电流方向
(1)用楞次定律判断
①楞次定律判断感应电流方向的步骤

②楞次定律中“阻碍”的含义:
|
|
|
|
阻碍原磁通量变化——“增反减同” | 阻碍相对运动——“来拒去留” | 使回路面积有扩大或缩小的趋势——“增缩减扩” | 阻碍原电流的变化——“增反减同” |
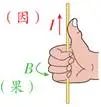
(2)用右手定则判断
楞次定律、右手定则、左手定则、安培定则的比较
应用的定则 | 安培(右手螺旋)定则 | 左手定则 | 右手定则 |
手势图 |
|
|
|
因果关系 | 电生磁 | 电受力 | 动生电 |
形象记忆 | “磁”的右半边“兹”螺旋写法,用右手螺旋; | “力”的最后一笔“丿”方向向左,用左手; | “电”的最后一笔“乚”方向向右,用右手。 |
2.感应电动势大小
情景图 |
|
|
|
|
法拉第电磁感应定律E=n | 回路(不一定闭合) | 一段直导线(或等效成直导线) | 绕一端转动的一段导体棒 | 绕与B垂直且在导线框平面内的轴转动的导线框 |
E= | E=BLv | E= | E=NBSωsin(ωt+φ0) |
【临考叮嘱】
①公式E=n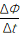 求解的是一个回路中某段时间内的平均电动势,在磁通量均匀变化时,瞬时值才等于平均值。
求解的是一个回路中某段时间内的平均电动势,在磁通量均匀变化时,瞬时值才等于平均值。
②公式E=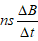 可用于计算平均感应电动势,此时
可用于计算平均感应电动势,此时 为一段时间磁感应强度的平均变化率;也可用于计算瞬时感应电动势,此时
为一段时间磁感应强度的平均变化率;也可用于计算瞬时感应电动势,此时 为某时刻磁感应强度的瞬时变化率,对应B-t图象中为某点的斜率,S为该时刻的有效面积;
为某时刻磁感应强度的瞬时变化率,对应B-t图象中为某点的斜率,S为该时刻的有效面积;
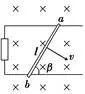
③有效性:E=Blv中的l为切割磁感线的导体棒的有效长度,即导体与v垂直的方向上的投影长度。
两个有效长度的区别
图例 |
|
|
|
E=Blv中的有效长度l | 为ab间的直线距离 | 为ab的投影长度lsinβ | 为ab长l |
安培力F=BIl中的有效长度l | 为ab间的直线距离 | 为ab长l | 为ab长l |
④相对性:E=Blv中的速度v是相对于磁场的速度,若磁场也运动时,应注意速度间的相对关系。
3.电磁感应中的电路问题
(1)解决电磁感应中的电路问题三部曲
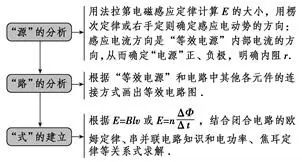
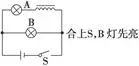
(1)电源正负极:导体棒可以等效为电源。在外电路,电流从正极流向负极;在电源内部,电流从负极流向正极。(如图甲)
(2)双电源:在分析双杆切割磁感线产生的感应电动势时,要注意是同向还是反向,可以根据切割磁感线产生的感应电流的方向来确定。(如图乙)

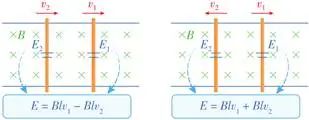
图甲图乙
(3)感应电量q=n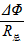 ,通过回路截面的电荷量q仅与n、ΔΦ和回路总电阻R总有关,与时间长短无关。
,通过回路截面的电荷量q仅与n、ΔΦ和回路总电阻R总有关,与时间长短无关。
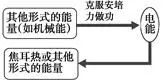
(4)能量转化及焦耳热的求法
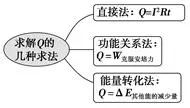
(1)能量转化 | (2)求解焦耳热Q的几种方法 |
|
|
4.电磁感应中的图像问题
(1)图像类型
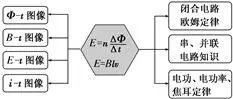
(2)分析方法

5.用“四步法”分析电磁感应中的动力学问题
(1)解决电磁感应中的动力学问题的一般思路是“先电后力”,具体思路如下:
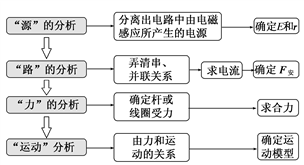
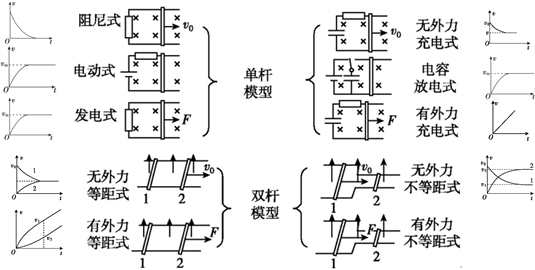
(2)导轨问题
近代物理
1.光电效应
(1)两条研究线索:

(2)定量分析光电效应时应抓住的三个关系式
①爱因斯坦光电效应方程:Ek=hν-W0.
②最大初动能与遏止电压的关系:Ek=eUc.
③逸出功与极限频率、极限波长λc的关系:W0=hνc=h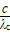 .
.
(3) 四类图象
图象名称 | 图线形状 | 由图线直接(间接)得到的物理量 |
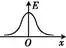
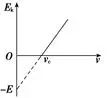
最大初动能Ek与入射光频率ν的关系图线 |
| ①极限频率:图线与ν轴交点的横坐标νc ②逸出功:图线与Ek轴交点的纵坐标的值W0=|-E|=E ③普朗克常量:图线的斜率k=h |
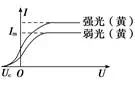
颜色相同、强度不同的光,光电流与电压的关系 |
| ①遏止电压Uc:图线与横轴的交点 ②饱和光电流Im:电流的最大值 ③最大初动能:Ekm=eUc |
颜色不同时,光电流与电压的关系 |
| ①遏止电压Uc1、Uc2 ②饱和光电流 ③最大初动能Ek1=eUc1,Ek2=eUc2 |
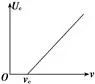
遏止电压Uc与入射光频率ν的关系图线 |
| ①截止频率νc:图线与横轴的交点 ②遏止电压Uc:随入射光频率的增大而增大 ③普朗克常量h:等于图线的斜率与电子电量的乘积,即h=ke.(注:此时两极之间接反向电压) |
2.波粒二象性
(1)个别光子的作用效果往往表现为粒子性;大量光子的作用效果往往表现为波动性。
(2)频率越低波动性越显著,越容易看到光的干涉和衍射现象;频率越高粒子性越显著,越不容易看到光的干涉和衍射现象,贯穿本领越强。
(3)光在传播过程中往往表现出波动性;在与物质发生作用时往往表现为粒子性。
(4)由光子的能量ε=hν,光子的动量p=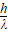 表达式也可以看出,光的波动性和粒子性并不矛盾:表示粒子性的粒子能量和动量的计算式中都含有表示波的特征的物理量——频率ν和波长λ。由以上两式和波速公式c=λν还可以得出:ε=pc。
表达式也可以看出,光的波动性和粒子性并不矛盾:表示粒子性的粒子能量和动量的计算式中都含有表示波的特征的物理量——频率ν和波长λ。由以上两式和波速公式c=λν还可以得出:ε=pc。
(5)物质波:任何一个运动着的物体,小到微观粒子大到宏观物体都有一种波与它对应,其波长λ= ,p为运动物体的动量,h为普朗克常量.
,p为运动物体的动量,h为普朗克常量.
3.玻尔的原子模型
(1)玻尔理论:
①轨道假设:原子中的电子在库仑引力的作用下,绕原子核做圆周运动,电子绕核运动的可能轨道是不连续的。
②定态假设:电子在不同的轨道上运动时,原子处于不同的状态,因而具有不同的能量,即原子的能量是不连续的。这些具有确定能量的稳定状态称为定态,在各个定态中,原子是稳定的,不向外辐射能量。
③跃迁假设:原子从一个能量状态向另一个能量状态跃迁时要放出或吸收一定频率的光子,光子的能量等于两个状态的能量差,即hν=Em-En。
(2)原子跃迁的两种类型
(1)原子吸收光子的能量时,原子将由低能级态跃迁到高能级态。但只吸收能量为能级差的光子,原子发光时是由高能级态向低能级态跃迁,发出的光子能量仍为能级差。
(2)实物粒子和原子作用而使原子激发或电离,是通过实物粒子和原子碰撞来实现的。在碰撞过程中,实物粒子的动能可以全部或部分地被原子吸收,所以只要入射粒子的动能大于或等于原子某两个能级差值,就可以使原子受激发而跃迁到较高的能级;当入射粒子的动能大于原子在某能级的能量值时,也可以使原子电离。
(3)关于能级跃迁的三点说明
(1)当光子能量大于或等于13.6 eV时,也可以被处于基态的氢原子吸收,使氢原子电离;当处于基态的氢原子吸收的光子能量大于13.6 eV,氢原子电离后,电子具有一定的初动能。
(2)当轨道半径减小时,库仑引力做正功,原子的电势能减小,电子动能增大,原子能量减小。反之,轨道半径增大时,原子电势能增大、电子动能减小,原子能量增大。
(3)一群氢原子处于量子数为n的激发态时,可能辐射出的光谱线条数:N=Cn2= 。
。
(4)巴耳末公式 =R(
=R(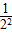 -
-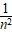 )n=3,4,5……式中n只能取整数,R称为里德伯常量R=1.10×107m-1。
)n=3,4,5……式中n只能取整数,R称为里德伯常量R=1.10×107m-1。
①巴耳末线系的4条谱线都处于可见光区。
②在巴耳末线系中n值越大,对应的波长λ越短,即n=3时,对应的波长最长;n=6时,对应的波长最短。
4.核反应类型与核反应方程
(1)核反应的四种类型
类型 | 可控性 | 核反应方程典例 | |
衰变 | α衰变 | 自发 |
|
β衰变 | 自发 |
| |
人工转变 | 人工控制 |
(卢瑟福发现质子) | |
(查德威克发现中子) | |||
| (约里奥·居里夫妇发现放射性同位素,同时发现正电子) | ||
| |||
重核裂变 | 比较容易进行人工控制 |
| |
| |||
轻核聚变 | 很难控制 |
|
(2).典型问题——原子核的人工转变与衰变的比较
原子核的衰变 | 原子核的人工转变 | |
发生反应的原子核 | 具有放射性的不稳定核 | 所有的原子核 |
反应条件 | 自发进行,无条件 | 利用α粒子、质子、中子或γ光子作为“炮弹”轰击靶核 |
反应本质 | 核子数变化,形成新核 | 核子的重组,形成新核 |
原子核的衰变 | 原子核的人工转变 | |
典型反应 |
|
|
核反应方程的特点 | 箭头左边只有一个放射性原子核 | 箭头左边有靶核和“炮弹”各一个 |
核反应的规律 | 质量数守恒(注意质量并不守恒),电荷数守恒 | |
书写方程的原则 | 尊重实验事实,不能仅仅依据守恒定律主观臆造 |
(3)解答有关核反应方程问题的技巧
(1)熟记常见基本粒子的符号——是正确书写核反应方程的基础.如质子(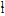 H)、中子(
H)、中子( n)、α粒子(
n)、α粒子( He)、β粒子(
He)、β粒子(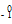 e)、正电子(
e)、正电子(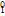 e)、氘核(
e)、氘核( H)、氚核(
H)、氚核(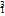 H)等.
H)等.
(2)掌握核反应方程遵守的规律——是正确书写核反应方程或判断某个核反应方程是否正确的依据,所以要理解并应用好质量数守恒和核电荷数守恒的规律.
(3)明白核反应过程是不可逆的——核反应方程只能用箭头连接并表示反应方向,不能用等号连接.
(4).三种射线

(5)半衰期
①定义:放射性元素的原子核有半数发生衰变所需的时间.
②影响因素:放射性元素衰变的快慢是由核内部自身的因素决定的,跟原子所处的化学状态和外部条件没有关系.半衰期是统计规律,对个别、少数原子无意义.
③公式:N余=N原·( )
) m余=m原·(
m余=m原·( )
) t表示衰变时间、τ表示半衰期.
t表示衰变时间、τ表示半衰期.
5.核能的计算方法
(1)根据ΔE=Δmc2计算时,Δm的单位是“kg”,c的单位是“m/s”,ΔE的单位是“J”.
(2)根据ΔE=Δm×931.5 MeV计算时,Δm的单位是“u”,ΔE的单位是“MeV”.
(3)根据核子比结合能来计算核能:原子核的结合能=核子比结合能×核子数.
(4)借助动量守恒和能量守恒计算.
6.比结合能与原子核稳定的关系:
(1)比结合能的大小能够反映原子核的稳定程度,比结合能越大,原子核就越难拆开,表示该原子核就越稳定。
(2)核子数较小的轻核与核子数较大的重核,比结合能都比较小,表示原子核不太稳定;中等核子数的原子核,比结合能较大,表示原子核较稳定。
(3)当比结合能较小的原子核转化成比结合能较大的原子核时,就可能释放核能。例如,一个核子数较大的重核分裂成两个核子数小一些的核,或者两个核子数很小的轻核结合成一个核子数大一些的核,都能释放出巨大的核能。
特别提醒:(1)结合能大的原子核,比结合能不一定大,结合能小的原子核,比结合能不一定小。
(2)核的大小与原子核稳定的关系方面:中等大小核的比结合能最大、原子核最稳定。
本文由小编发布,不代表一本线高考网立场,转载联系作者并注明出处:https://www.yibenxian.com/ziliao/56653.html





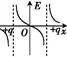


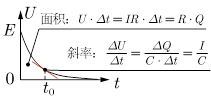









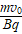 ,T=
,T=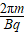
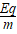 t
t t2
t2 T=
T=
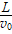 ,具有等时性
,具有等时性

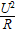 t,W=Q
t,W=Q
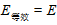
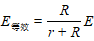

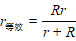

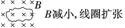






 U→
U→ Th+
Th+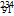 Pa+
Pa+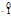 e
e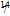 N+
N+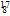 O+
O+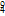 Be→
Be→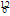 C+
C+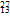 Al+
Al+ P+
P+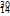 Si+
Si+ e
e U+
U+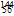 Ba+
Ba+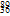 Kr+3
Kr+3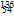 Xe+
Xe+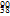 Sr+10
Sr+10 U→
U→ Th+
Th+